Nouveautés                                                                                                 Accueil      à propos de nous     Contacts      Liens    

Méthodologie d’analyse

QUESTIONS SOULEVÉES PAR UNE PHOTO

Authenticité du document analysé

L’authentification d’une photographie ou d’une vidéo est un élément primordial qui devrait faire partie intégrante de toute analyse, surtout lorsque l’identification du phénomène se révèle impossible.

Il n’existe cependant aucune « solution miracle clés en main » permettant d’affirmer que tel ou tel document est authentique ou pas. Diverses méthodes et techniques peuvent être utilisées afin de mettre en lumière d’éventuelles contradictions entre le témoignage visuel et le document, par exemple, mais on doit garder à l’esprit que l’appréciation de l’enquêteur analyste est indissociable de toute tentative d’authentification.

Par ailleurs, face à la progression exponentielle des moyens techniques disponibles permettant la falsification d’un document numérique, et aux difficultés nouvelles d’analyse qui en découlent, toute démarche d’authentification doit se faire de façon modeste et sans a priori, en gardant à l’esprit que le résultat ne sera jamais totalement certain.

Des outils spécifiques (logiciel IPACO) permettent cependant d’établir si un document photo/vidéo numérique constitue on non un original authentique, en s’appuyant sur l’analyse des nombreuses métadonnées qui l’accompagnent , certaines étant bien documentées (balises EXIF notamment), d’autres moins connues et plus difficiles d’accès, ainsi que sur la base de données techniques CamCAT intégrée dans IPACO.

En photographie argentique, un document original est nécessairement une pellicule (négatif noir et blanc, couleur ou diapositive). En photographie numérique, un fichier photo/vidéo est réputé original s’il résulte d’une simple copie directe (sous Windows, Linux, Mac OS…) du fichier d’origine créé dans la caméra, et si la photo/vidéo a été prise sans activer d’option de traitement ou d’incrustation en ligne.

Réalité d’un stimulus extérieur à l’appareil de prise de vue

Lorsque l’on observe, sur une photo, un objet ou un phénomène a priori non identifié, la première question qui se pose est de savoir si cette image résulte ou non d’un stimulus extérieur au système de prise de vue.

En effet, il existe de nombreux cas d’artefacts apparaissant sur des clichés, qui ne sont que le résultat d’effets parasites pouvant prendre naissance :

• dans l’optique de l’appareil :

 

• Saletés, gouttelettes ou petits grains de poussière sur l’objectif, apparaissant dans la photo comme des objets étranges ou de prétendus « orbes »
• réflexions internes (« lens flares ») produites à l’intérieur de la caméra
• fuites de lumière

• sur le capteur photosensible (le film en photographie argentique, la matrice de photosites en numérique) :

• Phénomène de « star effect » sur un film argentique, dû à une mauvaise manipulation au cours du développement, créant une tache étrange sur la photo
• Phénomène de « black sun », dû à une sursaturation des photorécepteurs dans une zone de lumière excessive, rendant moins de lumière que celle entrée dans l’objectif et causant l’apparition d’un « OVNI » noir circulaire (le plus souvent au centre d’un image directe du soleil)
• Phénomène de « burned pixel » faisant apparaître une tache brillante (généralement verte) là où il n’y a rien dans la scène

• dans le processus d’encodage (algorithme de compression destructive) du fichier image.

À cela s’ajoutent, comme nous l’avons vu précédemment, tous les cas de supercheries et de montages d’images que la micro-informatique moderne met désormais à la portée de tous.

La mise en évidence de l’absence de tout stimulus extérieur clôt définitivement l’analyse d’une photo.

Présence effective d’un objet matériel dans la scène

S’il peut être établi qu’il existait bien un stimulus extérieur au système de prise de vue, la question suivante est de savoir si celui-ci était lié à la présence physique d’un objet matériel dans la scène, ou au contraire à celle d’un phénomène immatériel, purement lumineux.

Dans la seconde hypothèse, il pouvait s’agir d’un phénomène naturel (atmosphérique, météorologique, astronomique) ou au contraire artificiel (phare, faisceau laser, hologramme).

Identification d’un phénomène

Que le stimulus soit un objet matériel ou non, le travail d’analyse du document vise essentiellement à en identifier la nature exacte, de façon certaine et définitive si c’est possible, ou – à défaut – avec une probabilité estimée.

L’identification définitive d’un phénomène passe par deux stades successifs : la conception d’une hypothèse recevable, puis la démonstration définitive de sa pertinence.

En pratique, pour l’investigateur, il s’agit dans un premier temps de chercher une explication rationnelle possible, par rapprochement avec des cas semblables ou avec des listes préétablies de stimuli déjà répertoriés. Cette étape peut aboutir à une explication plausible.

L’étape suivante consiste alors, dans la mesure du possible, à établir la preuve que cette explication est la bonne, à l’aide de données complémentaires ou d’un raisonnement irréfutable.

Caractérisation d’un phénomène non identifié

Dans le cas où la nature du phénomène ne peut vraiment pas être identifiée, l’objectif de l’analyse est de caractériser le plus objectivement et le plus précisément possible ce phénomène, à l’aide de paramètres quantitatifs mesurables à partir de la photo.

La poursuite des recherches pourra consister alors en une tentative de classification des différents dossiers inexpliqués, démarche propre aux sciences de l’observation.

DEUX APPROCHES TECHNIQUES COMPLÉMENTAIRES

Il existe deux approches distinctes – mais non exclusives – pour exploiter sur ordinateur un document photographique comportant un élément a priori non identifié. Ces deux approches sont bien connues dans le domaine militaire du renseignement d’origine image, où des vues du sol terrestre issues de satellites d‘observation, d’avions de reconnaissance ou de drones sont étudiées par des photo-interprètes (ou analystes d’images), à des fins de défense.

La première approche peut être qualifiée de qualitative et subjective. Elle consiste à manipuler interactivement l’image numérique « à l’instinct », pour tenter de mettre en évidence une piste de réflexion ou d’établir un rapprochement possible avec un environnement connu.

La seconde est quantitative et consiste à effectuer des mesures géométriques et radiométriques sur le fichier image, en s’appuyant autant que nécessaire sur les données complémentaires disponibles.

Analyse qualitative (Photo-interprétation)

La photo-interprétation d’un cliché consiste à le visualiser sur un écran tout en le « manipulant » de manière interactive, afin d’en distinguer les détails, d’en faire ressortir d’éventuelles particularités permettant d’orienter l’investigation et de spécifier les mesures à effectuer.

Au minimum, cette opération nécessitera quelques outils de traitement interactif classiques, comme on en trouve dans tous les logiciels de visualisation ou de traitement d’images. Elle constituera alors une première étape, avant celle de l’analyse quantitative, objet du paragraphe suivant.

Au mieux, l’opération de photo-interprétation se fera dans un environnement de PIAO (Photo-Interprétation Assistée par Ordinateur) de type IPACO, permettant à l’investigateur d’aborder simultanément les deux approches, qualitative et quantitative.

Analyse quantitative (Mesures et estimations)

Les mesures ou estimations que l’on peut effectuer de manière interactive sur une image numérique, à l’aide d’un ordinateur, se répartissent en deux domaines : géométrique et radiométrique.

Mesures géométriques

Ces mesures, comme leur nom l’indique, concernent des grandeurs telles que : angles, angles solides, distances, hauteurs, surfaces, volumes, vitesses, accélérations.

Les calculs mettent en jeu les caractéristiques de l’instrument de prise de vue, les réglages effectués pour la photo étudiée, d’éventuelles vérifications a posteriori sur le terrain, les positions relatives des pixels dans le fichier image.

Mesures radiométriques

Les mesures radiométriques utiles concernent d’une part la luminance des différents objets visibles sur le document photographique, traduite par les niveaux des pixels correspondants dans les 3 couleurs primaires, d’autre part la netteté des contours de ces objets, dépendant de la trajectoire de la lumière entre l’objet réel et le capteur photosensible (principalement à travers l’atmosphère et l’optique de l’appareil).

Évaluations de luminance

Les valeurs des pixels traduisent la luminance apparente des objets composant la scène photographiée, ainsi que la décomposition des flux lumineux dans les 3 couleurs primaires, le tout ayant été éventuellement altéré par les effets de la propagation atmosphérique et par les limitations de l’instrument optique.

De ces mesures, on peut en principe déduire des informations sur l’énergie émise, transmise ou réfléchie par l’objet, ainsi que, dans certains cas, des indications sur sa distance, compte tenu des modifications de luminance apparente que causent respectivement l’absorption et la diffusion atmosphériques.

Évaluations de netteté

On peut évaluer la netteté du contour apparent d’un objet en analysant la transition des niveaux de gris le long d’une perpendiculaire à ce contour, et en déduire des informations utiles sur les dégradations dues aux différents paramètres susceptibles d’avoir été mis en jeu : un éventuel effet de bougé, la profondeur de champ ou la diffusion atmosphérique.

DONNÉES EXPLOITABLES

Environnement général de la prise de vue

Toute photo a été prise à un endroit et à un moment précis. En fonction de l’évolution des investigations, une bonne connaissance de cet environnement spatio-temporel se révèle souvent indispensable.

Cela peut mettre en jeu de nombreuses données physiques mesurables, telles que la température, la pression atmosphérique, la visibilité horizontale, la vitesse et la direction des vents, la position des étoiles dans le ciel, la circulation aéronautique, d’éventuelles prévisions de rentrées atmosphériques, etc.

Scène photographiée

Dans les techniques d’imagerie numérique, on appelle scène la portion d’espace comprise dans le champ de l’appareil (angle solide) au moment de la prise de vue. En pratique, il s’agit donc de l’ensemble de ce qui est visible dans la photo.

La connaissance d’un maximum d’informations sur les éléments constitutifs de cette scène (taille réelle, distance de l’objectif, albédo d’objets de référence, identité des étoiles ou planètes observables, etc.) peut se révéler importante pour l’analyse du document.

Instrument et paramètres de prise de vue

Il est primordial de connaître le modèle d’appareil (ou de téléphone mobile) ayant permis la prise de vue, ainsi que les réglages éventuellement opérés par l’auteur de la photo, de façon à pouvoir retrouver les paramètres techniques indispensables à l’analyse, et dont les principaux sont rappelés ci-dessous. Ces informations sont en général fournies avec les données auxiliaires – ou métadonnées – associées au format standard des fichiers images générés par un appareil numérique.

Paramètres optiques

La partie optique et les réglages de l’appareil de prise de vue sont communs aux différents types d’appareils photo, argentiques ou numériques, même si les plages de valeurs peuvent parfois différer sensiblement.

Les principaux paramètres optiques sont rappelés ci-dessous.

Focale

La longueur focale sépare le centre optique de l'objectif du centre de la surface photosensible du capteur, lorsque la mise au point est faite sur l'infini. C’est donc la distance entre l’objectif et le plan focal image.

Toutes choses étant égales par ailleurs, plus la longueur focale est courte, plus le champ angulaire de vision est grand.

Si l’opérateur a, de façon délibérée, effectué la mise au point (focalisé) sur un objet particulier de la scène, la connaissance ou l’évaluation de la distance entre cet objet et l’objectif permettra d’être plus précis dans les calculs géométriques concernant la profondeur de champ.

Ouverture

L'ouverture réelle de l'objectif est égale au diamètre du diaphragme circulaire laissant passer la lumière durant le temps de pose, tel qu’il a été réglé (ou préréglé) pour la prise de vue.

L'ouverture – ou diaphragme – est habituellement définie à l’aide d’un facteur sans dimension appelé ouverture relative ou nombre d’ouverture, égal au quotient de la longueur focale par l’ouverture réelle du diaphragme. L’échelle des ouvertures normalisées forme une progression géométrique de raison √2 :

n =  1,0   1,4   2,0   2,8   4   5,6   8   11   16   22   32   45   64

Profondeur de champ

La profondeur de champ est la fourchette de distances de l’objectif à l’intérieur de laquelle les contours des objets photographiés dans la scène apparaissent avec netteté (hors flou de bougé).

Lorsque la mise au point a été faite sur l’infini (cas général), la profondeur de champ s’étend d’une limite inférieure, appelée distance hyperfocale, jusqu’à l’infini.

Dans le cas des appareils numériques, la limite inférieure de la profondeur de champ est souvent de l’ordre d’un mètre ou moins et la limite supérieure est généralement à l’infini.

Temps de pose

Le temps de pose (parfois appelé à tort vitesse) est la durée pendant laquelle le diaphragme reste ouvert pour réaliser la prise de vue. Selon les appareils, ce paramètre peut être choisi par l’opérateur ou imposé par un préréglage.

Portée du flash

La portée du flash définit la distance maximale de l’objectif à laquelle un objet de la scène peut être éclairé par le flash. C’est une donnée technique de la caméra.

Paramètres optoélectroniques

Dans un appareil numérique, la surface sensible (capteur) consiste en une matrice rectangulaire de photosites, sensibles à la lumière qu’ils convertissent en signal électrique. Le signal électrique issu de chaque photosite est mémorisé pour constituer un pixel de la photo.

La matrice de photosites joue un rôle équivalent à celui du rectangle de pellicule (par exemple 24x36) en photographie argentique.

La gestion de la couleur fait l’objet de codages différents selon les modèles d’appareil, mais on obtient toujours in fine trois valeurs par pixel, correspondant aux trois couleurs primaires : rouge, vert et bleu.

Dimensions du capteur

La connaissance des dimensions réelles de la surface sensible du capteur est déterminante pour l’évaluation du champ angulaire à partir de la longueur focale, de même que celle du nombre de photosites par ligne et par colonne, pour la localisation angulaire d’un point de la scène par rapport à l’axe de visée.

Les dimensions utiles du capteur peuvent être fournies directement, comme données techniques relatives à l’appareil, ou peuvent être calculées à partir d’autres données, en particulier du coefficient de conversion de focale : ce coefficient indique directement le rapport entre les dimensions de la matrice et le format de référence 24x36 mm de la photographie argentique (plus précisément : le rapport des diagonales).

Sensibilité du capteur

Contrairement au cas de la photographie argentique, où la sensibilité est entièrement déterminée par le film utilisé, la sensibilité d’un appareil numérique dépend essentiellement de la surface de ses photosites.

À cet égard, les appareils grand public, avec des pixels qui ne font que 2,8 à 4 μm de côté, ont une assez faible sensibilité (de l’ordre de 50 ISO ou moins), alors qu’il existe des appareils numériques à moyen ou grand capteur (pixels de 5 à 10 μm de côté) offrant des gammes de sensibilité nettement supérieures, pouvant atteindre des milliers d’ISO.

La valeur en ISO de la sensibilité d’un appareil numérique peut être fournie avec ses données techniques, ou extraite des métadonnées associées aux photos.

Réponse spectrale

Les capteurs au silicium ont intrinsèquement des réponses spectrales très différentes de celles de l’œil humain, ainsi que de celles des films argentiques. Leur sensibilité est très forte dans le rouge et l’infrarouge, moyenne dans le vert et très faible dans le violet et le bleu, ce que les constructeurs doivent compenser à l’aide de diverses techniques plus ou moins sophistiquées.

Pour des analyses très approfondies, il peut être utile de connaître la courbe de réponse spectrale de l’appareil de prise de vue, notamment lorsque l’hypothèse d’une contribution de l’ultraviolet ou de l’infrarouge est envisageable.

Remarque : c’est dans le domaine spectral que la photographie révèle ses plus sévères limitations comme outil d’aide à l’analyse des phénomènes lumineux rares observés dans l’atmosphère. En effet, des données qui seraient réellement multispectrales (voire hyperspectrales) constitueraient des informations scientifiques beaucoup plus riches sur l’origine et la nature de la lumière captée que de simples clichés en 3 couleurs (RVB).

Dans cette optique, l’utilisation de bonnettes de diffraction, adaptables aux appareils photo, permet d’obtenir, en superposition avec les photos prises, des données spectrales utiles sur les sources lumineuses présentes dans la scène (cf. Note technique n° 18 du GEPAN).

Image numérique

Une photo numérique se présente sous la forme d’un fichier image, dans un format standard donné (la plupart du temps JPEG). Ce fichier contient généralement des métadonnées, qui regroupent diverses informations sur l’appareil, la date de prise de vue et les réglages adoptés (métadonnées EXIF, IPTC, XPM notamment).

Ce fichier image peut être recueilli, dans son format d’origine, de différentes manières : directement sur son support physique (carte mémoire), par extraction de l’appareil via une connexion USB, ou sur n’importe quel autre support informatique sur lequel il a pu être copié (CD-Rom, clé USB, etc.)

En réalité, dans la mesure où le fichier n’a fait l’objet que de simples recopies, sans aucune modification de format (ni tricherie), le support informatique est indifférent car l’information exploitable reste rigoureusement la même (contrairement au cas des photos argentiques, pour lesquelles l’accès au négatif original est toujours primordial, en raison des dégradations d’information irrémédiables apportées par chaque étape du traitement).

Résolution géométrique

En simplifiant un peu, on peut considérer que, pour une taille donnée de matrice de photosites, la résolution géométrique est fonction du nombre total de pixels, en lignes et en colonnes.

En général, les appareils numériques proposent à l’utilisateur le choix entre différentes résolutions, exprimées en millions de pixels, ou mégapixels.

La valeur de la résolution adoptée pour une photo analysée est une donnée essentielle, qui peut être fournie par l’opérateur ou retrouvée a posteriori dans les métadonnées EXIF.

Résolution radiométrique

Chaque pixel est codé sur un nombre donné de bits, qui conditionne la résolution radiométrique du cliché. Le nombre de niveaux de gris (traduisant la luminance) et le nombre des nuances de couleur qu’il est possible de distinguer en dépendent directement.

Encodage et algorithme de compression

Les fichiers images sont parfois stockés en format brut (Raw), en vue d’un « développement numérique » ultérieur et réversible, mais le plus souvent ils sont compressés de façon irréversible au format JPEG, à l’intérieur de l’appareil.

Si le mode de compression est dit destructif, c’est-à-dire entraînant une perte d’information (cas du JPEG), il peut en résulter l’apparition d’artefacts sur la photo (le plus souvent des moirés de couleur).

Ces détériorations de la qualité de l’image sont alors d’autant plus marquées que le taux de compression choisi est élevé.

Métadonnées

Comme nous l’avons vu, les fichiers générés par un appareil numérique (en général au format JPEG) contiennent, en plus des lignes et colonnes de pixels, un certain nombre de données auxiliaires ou métadonnées (EXIF, IPTC, XPM…). On y retrouve les caractéristiques du fichier lui-même, mais aussi celles de l’appareil ainsi que la datation et les paramètres de réglage de la prise de vue. Des emplacements sont également prévus, dans la définition de ce format, pour diverses données complémentaires, notamment de localisation GPS.

L’extraction de ces données – précieuses pour l’analyse – est possible grâce à des logiciels spécialisés, dont beaucoup sont accessibles gratuitement sur Internet. Dans la plupart des cas, elles sont suffisantes pour conduire l’analyse, même en l’absence d’informations fournies par le témoin sur l’appareil qu’il a utilisé. Le logiciel IPACO permet à l’analyste de déterminer, grâce aux métadonnées, si une photo numérique au format JPEG est un original ou non, et lui fournit tous les éléments disponibles pour estimer la probabilité d’une fraude.

PARAMÈTRES MESURABLES SUR UNE PHOTO

Les paramètres qu’il est possible de mesurer à partir d’une photo appartiennent à deux domaines : géométrique et radiométrique.

Les paramètres géométriques – angles, tailles ou distances – mettent en jeu la position, en lignes et en colonnes, des pixels dans la photo, alors que les paramètres radiométriques sont calculés à partir des niveaux associés aux pixels.

Paramètres géométriques

La photographie repose sur un principe de projection conique et d’intégration temporelle, permettant de représenter par une image à 2 dimensions une information réelle occupant un espace à 4 dimensions (espace et temps). Il est donc a priori impossible de reconstituer la totalité de la géométrie des éléments d’une scène à partir d’une simple photo, sauf si l’on dispose d’informations complémentaires (autres photos réalisées sous un autre angle, ou données issues d’autres sources).

En particulier, si la position des pixels dans la photo permet toujours, dans la mesure où les données techniques indispensables sont disponibles, de calculer les dimensions angulaires d’un objet, l’évaluation de ses dimensions réelles n’est possible que dans la mesure où l’on peut connaître ou estimer la distance qui séparait cet objet de l’objectif au moment de la prise de vue.

Nous allons aborder successivement la distance angulaire d’un point donné par rapport à l’axe de visée et la mesure d’une dimension angulaire d’un objet. Puis, après avoir rappelé comment on peut en déduire une dimension linéaire à partir de la distance de l’objectif, nous passerons en revue différentes façons d’approcher l’estimation de cette distance ou, à défaut, d’une plage de valeurs possibles.

Pour pouvoir effectuer les calculs relatifs à la distance angulaire, par rapport à l’axe de visée, d’un point de la scène représenté par un point A sur le support, ou relatifs à la distance angulaire  entre 2 points de la scène représentés par les points A et B sur le support, il faut disposer de plusieurs données géométriques : la longueur focale f utilisée pour la prise de vue, et les distances d, a et b, mesurées sur le support photosensible (film argentique ou matrice de photosites), définies comme suit :

f  : longueur focale

a  : mesure de la distance PA sur le support sensible

b  : mesure de la distance PB sur le support sensible

d  : mesure de la distance AB sur le support sensible

O : centre optique de l’objectif de l’appareil de prise de vue

P : centre de la photo, sur le support sensible

   

                                                                                                                 

                                                                                                                                   

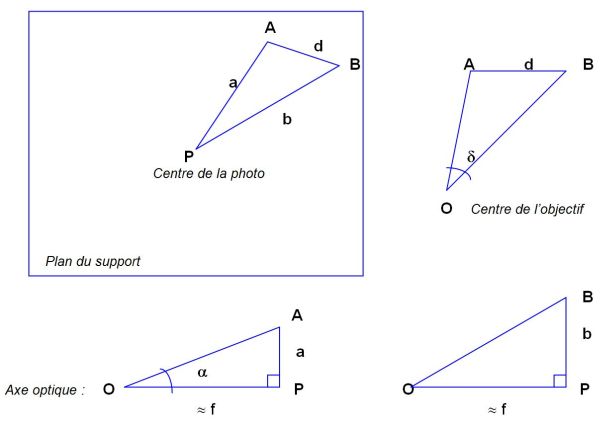
Localisation angulaire d’un objet dans la scène

À l’intérieur de l’angle solide qui définit le champ angulaire de l’appareil au moment de la prise de vue, et donc les contours de la scène, il est aisé de déterminer la distance angulaire  d’un point donné A de l’image par rapport à l’axe optique :

 = arctan (a/f)

On pourra dans certains cas, à l’aide de données complémentaires, en déduire une estimation d’altitude si l’axe de visée est connu, et notamment s’il est proche de l’horizontale.

Dimensions angulaires d’un objet

Dans l’hypothèse où la distance entre les points d’intérêt dans la scène et l’appareil de prise de vue est très supérieure à la longueur focale (ce qui est pratiquement toujours vérifié, en dehors de la macrophotographie), on admet l’approximation :

OP  f

Par application au triangle OAB du théorème de Pythagore généralisé, on calcule la taille angulaire  de l’objet comprise entre les points A et B à l’aide de la formule :

                 2 f2 + a2 + b2 – d2

 = Arccos [ ___________________ ]

                  2√ {(f2 + a2) (f2 + b2)}

Dimensions d’un objet

Pour pouvoir mesurer – ou estimer – la dimension D d’un objet dans une direction donnée, perpendiculaire à l’axe de visée, il faut disposer préalablement de la mesure – ou de l’estimation – de deux données : la dimension angulaire  de l’objet dans cette direction et la distance x qui le sépare de l’objectif.

                                                                                 

                                                                                

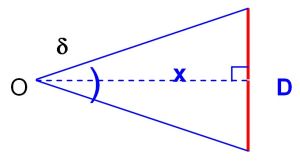
La relation applicable est alors :

D = 2x x tan (/2)

Estimation de la distance d’un objet

La distance entre l’objet étudié et l’objectif de l’appareil ne peut évidemment pas être directement mesurée à partir de la photo, mais différentes approches analytiques permettent de l’estimer, ou au minimum de lui fixer des valeurs limites possibles.

Estimation à partir d’autres objets identifiés et localisés

Si la configuration des éléments de la scène permet de savoir que la distance entre l’objectif et l’objet étudié est comprise entre des distances limites connues ou mesurables sur site, on en déduit aisément une fourchette de dimensions possibles pour l’objet, à partir de ses dimensions angulaires.

Selon les cas, les objets de référence pourront être des bâtiments, des nuages, de la végétation, etc.

Prise en compte de l’ombre portée

Si l’objet étudié est accompagné d’une ombre portée visible sur la photo, on pourra tenter d’en tirer des déductions d’ordre géométrique, notamment si la source de lumière (le soleil dans la plupart des cas) peut être localisée par rapport à la scène, ou si les ombres d’autres objets de cette scène peuvent également être repérées.

Analyse de la profondeur de champ

La profondeur de champ définit la plage de distances entre l’objectif et l’objet pour lesquelles la photo est nette (hors flou de bougé). Elle fixe donc, si l’objet apparaît avec netteté, les limites possibles pour la distance entre cet objet et l’objectif.

Ce paramètre permet parfois de mettre en évidence une incompatibilité entre la netteté – ou le flou – des contours d’un objet, d’une part, et la distance de l’objectif à laquelle était censé se trouver cet objet, d’autre part (exemple des « orbes »).

Lorsque la mise au point a été faite sur l’infini, ce qui est le cas pour la plupart des photos prises à l’aide d’un appareil numérique, la profondeur de champ s’étend de la distance hyperfocale à l’infini. Dans ce cas, seuls des objets « trop près » de l’objectif peuvent se trouver en dehors de la profondeur de champ, donc flous de ce fait.

La distance hyperfocale H se calcule comme suit :

H = f2 / (n x e)

f  : longueur focale

n  : nombre d’ouverture

e  : cercle de confusion ou netteté admissible .

Le paramètre e est plutôt subjectif par nature. Dans la pratique, on lui attribue une valeur de l’ordre de 0,03 mm en photographie argentique et, dans le cas d’un appareil numérique, une valeur égale à la taille de 2 pixels (en général de l’ordre de 0,01 à 0,02 mm).

Si la mise au point a été faite sur un objet situé à une distance D, les limites de la profondeur de champ peuvent être calculées comme suit :

PdC = Dp – Da

Da = (H x D) / (H + D)  

    

Dp = (H x D) / (H – D)

PdC : profondeur de champ

Da       : distance antérieure (limite inférieure de la profondeur de champ)

Dp       : distance postérieure (limite supérieure de la profondeur de champ)

Effet de la propagation atmosphérique sur la luminance apparente

Sur une photo réalisée de jour, notamment sous une lumière diffuse (ciel couvert), l’exploitation des lois de propagation (absorption et diffusion) de la lumière permet parfois, à partir de mesures ou d’estimations de luminance apparente basées sur les niveaux des pixels, d’évaluer des plages de distances possibles entre un objet observé sur la photo et l’appareil de prise de vue. Les principales équations sur lesquelles repose cette approche sont présentées plus loin.

Effet de la diffusion atmosphérique sur la netteté

En fonction des conditions météorologiques, les effets de la diffusion atmosphérique sur la netteté apparente des contours peuvent être mis en évidence et comparés entre divers objets de référence et l’objet analysé, ce qui permet alors de définir une plage de distances possibles séparant cet objet de l’appareil.

Portée du flash

Sur une photo prise de nuit, si un objet apparaît illuminé par le flash, sa distance de l’objectif ne peut pas être supérieure à la portée de ce flash.

Vitesse transversale d’un objet

Pour pouvoir mesurer – ou estimer – la vitesse transversale moyenne V d’un objet durant un intervalle de temps Δt et dans une direction donnée, perpendiculaire à l’axe de visée, il faut disposer préalablement de la mesure – ou de l’estimation – de deux données : la mesure angulaire  de la portion de trajectoire décrite par l’objet au cours de Δt dans cette direction, et la distance x qui le sépare de l’objectif. Il faut également disposer de données images correspondant aux deux instants bornant l’intervalle de temps Δt.

Trois cas peuvent se présenter :

• 1 photo montrant la portion de trajectoire quasi rectiligne d’un petit objet se déplaçant de façon significative durant le temps de pose (égal à Δt), prise par une caméra supposée fixe. La portion de trajectoire pourra faire l’objet d’une mesure angulaire.

• 2 photos de l’objet étudié, prises successivement par une caméra supposée fixe, à deux instants connus (séparés de Δt). Ces deux photos pourront être superposées et la portion de trajectoire mesurée.

• 1 vidéo prise par une caméra supposée fixe, dont on extrait 2 images séparées de Δt pour se ramener au cas précédent.

Si la portion de trajectoire a une longueur égale à L, la vitesse transversale a pour valeur :

V = L / Δt

Paramètres radiométriques

Luminance d’un objet

La luminance associée à un objet photographié est homogène à une puissance émise par unité de surface et par unité d’angle solide dans la direction de l’objectif. Elle s’exprime en lm/sr/m2 (lumen par stéradian par mètre carré), la correspondance entre lumen et watt dépendant, pour chaque longueur d’onde, de l’efficacité lumineuse du rayonnement.

Cette luminance observée peut être due à une émission lumineuse propre de l’objet, à une transmission (objet transparent ou translucide) ou à une réflexion de la lumière venant d’ailleurs, en particulier du soleil.

Dans le cas d’un objet non lumineux, on pourra évaluer son albédo : fraction du flux lumineux reçu réfléchie par l’objet, dont la valeur va de 0 pour un corps noir à 1 pour un corps blanc. Une évaluation de l’albédo pourra parfois, par rapprochement, fournir des indications sur le matériau constitutif de l’objet étudié.

Le flux lumineux F (exprimé en lumens) – émis, transmis ou réfléchi par l’objet – est modifié simultanément de deux façons par l’atmosphère environnante :

• La propagation atmosphérique, entre l’objet et l’appareil de prise de vue, induit une atténuation due à l’absorption atmosphérique par les molécules d’air, selon la loi de Bouguer :

F = F0 10-x

où  est le coefficient d’extinction et x l’épaisseur traversée.

La valeur de  dépend des conditions météorologiques et de la longueur d’onde, et la quantité x représente la             densité optique de l’épaisseur atmosphérique considérée.

Pour des sources lumineuses qui se situent au-delà de l’atmosphère (objets astronomiques, satellites),             l’atmosphère intervient dans toute son épaisseur, qui ne dépend que de la distance zénithale de la source.

L’intensité de la source varie alors en fonction de cette distance zénithale selon une « droite de Bouguer ».

• Dans le cas des photos prises de jour, à la luminance propre L d’un objet situé dans la basse atmosphère à la distance x de l’objectif, atténuée par l’absorption atmosphérique comme indiqué précédemment, s’ajoute une contribution de la diffusion atmosphérique de la lumière du jour.

Si LH représente la luminance du ciel à l’horizon (x  ), la luminance apparente L’ de l’objet est donnée par la             relation :

L’ = 10-x L + (1 - 10-x) LH

où le premier terme représente l’extinction de la lumière issue de l’objet, le second représentant la contribution             de la diffusion atmosphérique.

S’il s’agit d’un objet noir (ou très sombre), la formule se simplifie pour devenir :

L’ = (1-10-x) LH

Dans le cas particulier d’un objet d’albédo R, sous un ciel uniformément couvert, on vérifie :

L’ = [1 – (1 – R/2) 10-x ] LH

Les données directement mesurables quantifiant la lumière reçue par un pixel donné de l’image numérique sont le niveau de gris (en noir et blanc) et les niveaux respectifs dans les 3 couleurs primaires (rouge, vert, bleu). Ces valeurs traduisent la luminance apparente des points correspondants de la scène mais, s’il est vrai qu’en photographie argentique, ainsi qu’en numérique dans le cas du format RAW (brut), il est parfois possible d’établir une formule de correspondance – plus ou moins empirique – entre la luminance et le niveau de gris, grâce à des calculs de lumination, cela devient quasiment impossible avec le format JPEG, en raison de tous les traitements d’optimisation effectués à la volée par l’appareil avant mémorisation de l’image (dématriçage du RVB, délinéarisation avec application d’un facteur de gamma, compression, accentuation, etc.).

À défaut de pouvoir évaluer des valeurs absolues de luminance, les seuls calculs possibles sont relatifs, et exploitent le caractère monotone de la variation du niveau de gris en fonction de la luminance apparente.

Ces interpolations ou extrapolations empiriques sont néanmoins précieuses dans de nombreux cas, car elles permettent de cerner des plages de distances possibles d’un objet, par comparaison avec d’autres éléments de la scène situés eux-mêmes à des distances connues.

Netteté d’un objet

L’évaluation de la netteté (ou du flou) du contour apparent d’un objet peut être déterminante dans le cadre de plusieurs approches bien distinctes.

• Flou de bougé : si, lorsque la photo a été prise, l’objet analysé était en mouvement et si cela se traduit par un flou de bougé, il est envisageable de quantifier sa vitesse angulaire au moment de la prise de vue, à partir de la mesure angulaire du bougé et du temps de pose

• Profondeur de champ : si un certain flou est attribuable au fait que l’objet se situait en dehors de la profondeur de champ, on peut en déduire des limites possibles pour la distance entre l’objet et l’appareil (cf. plus haut)

• Diffusion atmosphérique : indépendamment de ses conséquences sur la luminance apparente d’un objet, la diffusion atmosphérique a des effets de dégradation sur la netteté des contours (FTM), d’autant plus importants que l’objet est éloigné. Cette propriété est plus ou moins visible, et donc mesurable, en fonction des conditions météorologiques. Dans les cas favorables (temps couvert) il est, là aussi, possible d’en déduire des limites de distances possibles par comparaison avec d’autres objets de la scène, dont on sait estimer la distance au moment de la prise de vue.

 

   

Couleur d’un objet

La couleur d’un objet peut se révéler utile pour son analyse, en fournissant une information (limitée) sur le spectre de la lumière émise, transmise ou réfléchie par l’objet. Par ailleurs, sa comparaison avec la couleur dominante de la scène permet de mettre en lumière une éventuelle incohérence pouvant servir de preuve de l’existence d’un trucage par incrustation.

Texture d’un objet

L’objet analysé, s’il représente une surface suffisante sur la photo, peut éventuellement laisser apparaître une texture, qui dépend du matériau dont il est constitué ou revêtu.

Un logiciel de traitement d’images permettra dans ce cas de caractériser cette texture, en vue d’une comparaison, si nécessaire, avec un catalogue de textures de référence.

ANALYSE D’UNE SÉQUENCE VIDÉO

Le contenu d’une séquence vidéo peut être considéré soit comme un enchaînement de photos individuelles, analysables séparément comme autant de documents statiques, soit comme la représentation dynamique d’un mouvement.

Analyse image par image

Les outils de traitement numérique de la vidéo permettent tous l’extraction d’une image isolée, qui peut alors être exploitée comme une simple photo. L’intérêt dans ce cas réside dans le grand nombre d’images parmi lesquelles on peut choisir celle(s) qui offre(nt) l’information la plus riche et la plus exploitable.

La limitation de cette approche tient à la résolution de ces images, généralement inférieure à celle des photos que génère un appareil numérique.

Désentrelacement

Généralement, les images constitutives d’un signal vidéo sont formées par addition de deux trames saisies alternativement, l’une étant codée sur les lignes impaires de l’image, l’autre sur les lignes paires.

Dans le cas de l’étude d’un mouvement rapide (changement d’aspect significatif entre deux images successives), l’opération de séparation des trames – ou « désentrelacement » – apporte en pratique une amélioration de la résolution temporelle par un facteur 2.

Chaque trame individuelle permet alors, par interpolation verticale, la reconstitution d’une image, qui peut être analysée séparément.

Accumulation d’images

Dans le cas particulier où une vidéo montre un objet relativement immobile, mais difficile à distinguer en raison d’un bruit de fond important ou d’un trop faible contraste, on peut envisager une opération d’accumulation de plusieurs images successives : après les avoir recalées au mieux entre elles par rapport à l’objet étudié, on effectue une addition de ces images, ce qui a pour effet de rehausser le rapport signal/bruit et donc d’améliorer la lisibilité de l’objet.

Analyse du mouvement

Le propre de la vidéo, par opposition avec la photo, est d’enregistrer le mouvement. Dans le cadre de l’étude des PAN, un document de ce type fournit des informations dynamiques : vitesse de déplacement, accélération, déformation, changement de forme ou de couleur de l’objet étudié.

Pour de telles analyses, la connaissance des paramètres relatifs à la dimension temporelle (nombre d’images par seconde, système de tramage) est essentielle.

Malheureusement, dans l’état actuel, les métadonnées associées aux vidéos numériques ne font pas l’objet d’une normalisation équivalente à celle des métadonnées EXIF pour la photo.

MÉTHODOLOGIE PRATIQUE D’ANALYSE

Ce chapitre récapitule la séquence standard des actions à prendre pour conduire l’analyse d’une photo présumée de PAN.

Il sera illustré, de paragraphe en paragraphe, par le suivi en italiques du traitement d’un dossier particulier.

On pourra également se reporter à l’exemple concret que constitue le dossier photographique présenté à la fin du rapport d’étude au GEPAN de 1982, où la mise en évidence et la reconstitution d’une supercherie avaient pu être effectuées par le biais de 6 approches techniques différentes, mettant en jeu les principes évoqués dans le présent document.

Illustration : le dossier qui a été choisi pour illustrer – dans les limites du possible – les différentes étapes de l’analyse d’une photo, a pour cadre la compétition de montgolfières Mondial Air Ballon 2007 qui a eu lieu, comme tous les ans, sur l’ancienne base militaire de Chambley-les-Bussières (Meurthe-et-Moselle) en août 2007.

L’un des participants à cette manifestation, qui avait pris 120 photos avec son appareil photo numérique Nikon D200, en a extrait une, datée du 5 août, sur laquelle apparaissait en haut à gauche dans le ciel, parmi les montgolfières, un objet très différent et non identifié.

Ce cas nous a été rapporté par M. Christian Comtesse, qui lui a consacré une enquête approfondie sur le terrain dont les conclusions seront présentées plus loin.

Voici la photo – que nous analyserons – telle quelle, ainsi qu’un zoom sur l’objet non identifié :

Photo de Chambley

Zoom sur l’objet non identifié de Chambley

Recueil des données externes

Localisation spatio-temporelle de la photo

Les premières informations requises pour l’analyse d’une photo concernent le lieu, la date, et l’heure précise où elle a été prise.

Selon les besoins de l’enquête, on pourra affiner la connaissance du lieu où se trouvait l’appareil en s’appuyant, si besoin est, sur une carte détaillée ou un GPS, dans le cadre d’une éventuelle reconstitution in situ.

En ce qui concerne la date, il sera prudent de noter non seulement l’heure locale mais aussi l’heure universelle, la différence entre les deux étant fonction du lieu et de la saison.

Il est important de mettre en application un grand principe de la mesure en physique : pour chacune de ces données, il n’est pas suffisant de recueillir une valeur (longitude, latitude, heure), mais il faut pouvoir lui associer une incertitude. En particulier en ce qui concerne l’heure de prise de vue, on essaiera de quantifier la marge d’erreur possible en fonction de la source d’information (la montre du photographe, la date indiquée dans les métadonnées EXIF, etc.), si nécessaire en effectuant des recoupements  et des calibrations a posteriori.

Illustration : dans le cas de Chambley, toutes les données de localisation dans l’espace (lieu de la compétition) et dans le temps (19h14, heure locale) ont été fournies spontanément par l’auteur de la photo – prise à contre-jour en fin de journée, par très beau temps.

On notera cependant un désaccord sur l’année, entre le témoignage (2007) et la datation enregistrée avec les métadonnées EXIF (2006). Il s’agit probablement d’une erreur de saisie initiale sur l’appareil de la part de l’opérateur.

Données d’environnement

Les données d’environnement à rechercher en priorité diffèrent, bien entendu, en fonction des cas, et notamment en fonction de l’heure de prise de vue (de jour ou de nuit).

Extérieur jour

Pour une photo réalisée de jour et à l’extérieur, notamment si le phénomène apparaît dans le ciel, il sera utile de connaître la valeur des paramètres météorologiques classiques : température, pression, humidité, vitesse et direction des vents, visibilité horizontale.

Ces paramètres seront recueillis auprès des sources habituelles, en particulier : Météorologie nationale, aéroports et aérodromes avoisinants.

Extérieur nuit

Pour une photographie réalisée de nuit sous un ciel suffisamment clair, on s’efforcera d’obtenir un tracé de la configuration de la voûte étoilée telle qu’elle apparaissait dans le champ de l’objectif au moment de la prise de vue.

Plusieurs logiciels spécialisés permettent de réaliser de tels tracés en fonction des coordonnées géographiques du lieu d’observation et de l’heure universelle.  

Dans tous les cas, si une confusion est possible, il faudra rechercher les informations disponibles sur le trafic aérien ou les prévisions de rentrées atmosphériques (météorites, débris spatiaux) au moment de la prise de vue. De même en ce qui concerne d’éventuels éclairages inhabituels, tels des faisceaux laser dirigés vers le ciel (fête foraine, rave-party, bateaux-mouches ou autres) ou des lâchers de lanternes thaïlandaises.

Données sur la scène photographiée

En fonction des circonstances et de l’environnement, on essaiera d’identifier les éléments apparaissant dans le champ de la photo – surtout ceux qui peuvent servir de points de comparaison géométrique ou radiométrique – et de leur associer des dimensions chiffrées (tailles, distances de l’appareil, surfaces), en vue de calculs d’interpolation ou d’extrapolation, ainsi que des caractéristiques de luminance et de couleur.

Il peut s’agir, par exemple, de bâtiments, d’arbres, de reliefs, de corps célestes (soleil, lune), de personnes.

Illustration : les seuls éléments de comparaison visibles dans la scène photographiée à Chambley sont des montgolfières. Il était donc important de se renseigner sur la taille de ces objets.

Une recherche sur Internet a permis de savoir qu’une montgolfière courante avait un volume de l’ordre de 2500 m3, avec une hauteur de 20 m et un diamètre de 15 m.

Témoignages et autres enregistrements

Il va de soi que toutes les informations disponibles sur le « cas » étudié doivent être recherchées, pour pouvoir effectuer des recoupements, d’éventuelles triangulations, des évaluations de taille ou de vitesse, etc.

Remarque : Il est utile de rappeler l’une des recommandations émises par le groupe de scientifiques réunis à Pocantico en 1997, pour un colloque international sur « Les traces physiques associées aux témoignages d’ovnis ». En substance, elle stipulait qu’un dossier PAN ne mérite d’être étudié avec sérieux que s’il existe au moins deux sources d’information indépendantes.

Ce principe implique donc, dans le cas d’une photo, que pour justifier la réalisation d’une analyse approfondie, il faut qu’il existe au minimum un témoignage oculaire ou un autre enregistrement – photographique ou autre – recueilli indépendamment de cette photo.

Illustration : la photo de Chambley a été rapidement connue dans les milieux ufologiques et la presse locale, ce qui a permis de rassembler plusieurs autres clichés pris à l’occasion du Mondial Air Ballon 2007. Plusieurs semblent sans rapport avec le premier (quelques-uns sont farfelus), mais il existe une seconde photo (voir ci-dessous) qui semble bien montrer le même objet, un peu au-dessous de la nacelle d’une montgolfière.

Autre photo de Chambley

Recueil des données techniques

Caractéristiques de l’appareil de prise de vue

Toutes les données techniques sur l’appareil de prise de vue et les éventuels réglages effectués pour réaliser la photo (focale, distance de mise au point, temps de pose) doivent être recueillies.

À partir du modèle précis d’appareil, il est toujours possible d’en retrouver toutes les caractéristiques, car si l’auteur de la photo n’en dispose pas lui-même, le constructeur pourra être consulté.

Par ailleurs, les fichiers images issus d’appareils numériques sont, de plus en plus systématiquement, porteurs de métadonnées au format EXIF, qui fournissent tous les paramètres requis sur l’appareil, la date et les réglages de prise de vue. L’accès aux métadonnées originelles n’est toutefois possible que si le fichier image produit par l’appareil n’a pas subi de transformation.

En outre, il existe un certain nombre de redondances et donc des moyens de reconstituer certaines données si elles s’avéraient manquantes : par exemple, les dimensions réelles de la matrice photosensible peuvent être aisément reconstituées à partir du coefficient de conversion de focale, lorsque ce paramètre est disponible.

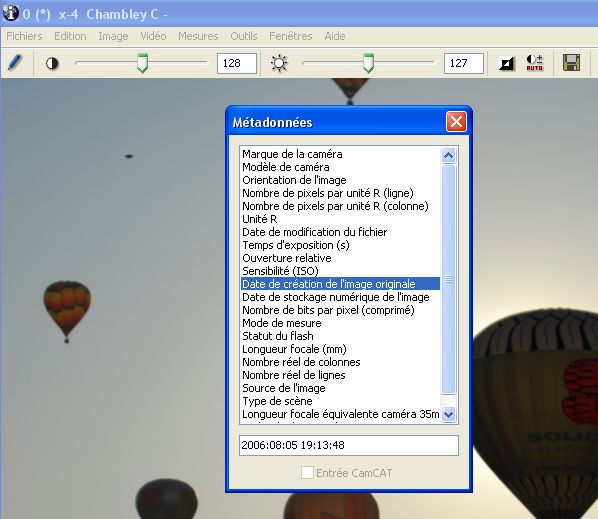
Illustration : la photo de Chambley a été obtenue dans son format original, ce qui a permis la récupération des métadonnées EXIF, en plus des informations détaillées déjà fournies par son auteur.

Paramètres de prise de vue

Les paramètres qui correspondent aux réglages et mises au point éventuellement effectués par l’opérateur doivent être recueillis auprès de lui dans la mesure du possible.

De plus, comme indiqué précédemment, on pourra généralement retrouver ces données dans les métadonnées du fichier image.

Dans le cas particulier de la distance de mise au point, si l’opérateur se rappelle avoir pris sa photo en réglant la netteté sur un objet donné, il pourra se révéler utile de connaître ou d’estimer la distance réelle entre cet objet et l’appareil de prise de vue, en vue de calculs précis sur la profondeur de champ.

Illustration : la photo de Chambley a été prise du sol, avec un appareil reflex numérique Nikon D200 réglé sur l’infini, avec un temps de pose de 1/6400 s.

Recueil du fichier image et de ses métadonnées

Comme cela a été expliqué précédemment, le fichier image devra impérativement être recueilli dans son format d’origine, après n’avoir fait l’objet, au maximum, que de recopie(s) informatique(s), sans aucune modification.

On utilisera les différents médias disponibles : de préférence la carte mémoire de l’appareil (pour être – en principe – certain qu’aucune transformation n’a pu être opérée en dehors de cet appareil photo, ou à défaut tout autre support informatique (clé USB, CD-Rom).

Fichier issu d’un appareil photo numérique

Pour avoir accès aux données auxiliaires gérées dans le format, on fera appel à des logiciels spécialisés. Dans le cas – très largement majoritaire – du format EXIF, il existe de nombreuses solutions logicielles pour extraire les métadonnées, parmi lesquelles : Exifer, GeoSetter, XnView, ACDSee, Imatch, PhotoME, et enfin « IrfanView » (ce dernier, complété par le plug-in « EXIF », a été recommandé par le comité JPEG [www.jpeg.org]).

L’auteur de ce rapport travaille avec IPACO, qui permet à la fois d’afficher les valeurs des paramètres EXIF présents dans une image, et d’exploiter automatiquement ces mêmes paramètres pour effectuer rapidement des mesures angulaires.

Fichier issu d’un téléphone mobile

Dans le cas d’une photo issue d’un téléphone mobile, la question qui se pose au départ est celle de la récupération du fichier image (généralement au format JPEG) dans un ordinateur.

Trois modes de transfert sont possibles, en fonction des modèles :

• Recueil d’une carte mémoire externe, de type Memory Stick ou Secure-Digital, lisible sur un lecteur de cartes connecté à l’ordinateur

• Transfert direct du téléphone à l’ordinateur par USB, à condition que ce type de connexion soit fourni en Plug and Play, ou qu’un logiciel pilote bien adapté soit disponible

• Transfert direct du téléphone à l’ordinateur par Bluetooth (ondes radio à courte distance).

De plus en plus de modèles de téléphones mobiles équipés d’un appareil photo numérique génèrent des fichiers images au format JPEG, avec des métadonnées EXIF, ce qui ramène l’analyste au cas d’un appareil standard.

Avec les smartphones, un transfert simple et direct par e-mail est proposé.

Authentification du document

Cohérence des données physiques

Une analyse du témoignage et de sa concordance avec les paramètres physiques du document est dans tous les cas nécessaire. Elle pourra mettre en jeu des outils de vérification spécialisés externes, tels que les données METAR pour la météorologie, Google Images pour la recherche d’images existantes, ou Stellarium pour l’astronomie.

L’étude de la cohérence des ombres et des lumières dans l’ensemble de la prise de vue est également un préalable indispensable. Elle pourra se faire en déterminant en premier lieu la ou les sources lumineuses, et en vérifiant à l’aide d’un outil interactif spécialisé de type IPACO la cohérence de leur aspect et de leur impact sur les ombres propres et portées.

Support argentique

Il existe peu de moyens de recoupement, dans une démarche d’authentification, entre une photo argentique et le témoignage qui l’accompagne, sachant que la règle fondamentale incontournable est de ne travailler qu’à partir de documents originaux.

Néanmoins certaines informations incrustées dans une pellicule développée dans un laboratoire public peuvent se révéler précieuses pour mettre en défaut un faux témoignage : d’une part la date de développement, inscrite en bord de film, d’autre part la numérotation séquentielle des clichés, ces données étant a priori infalsifiables.

Support numérique

Métadonnées EXIF

Comme nous l’avons déjà vu, il est primordial de connaître le modèle d’appareil ayant permis la prise de vue, ainsi que les réglages éventuellement opérés par l’auteur de la photo, de façon à pouvoir retrouver les paramètres techniques indispensables à l’analyse. Ces informations sont en général fournies par les données auxiliaires – ou métadonnées – associées au format standard des fichiers images générés par un appareil photo numérique.

Ces métadonnées EXIF sont supportées par tous les formats de fichiers images, à l’exception de JPEG2000 et PNG. Elles comprennent de nombreuses balises, définissant aussi bien les données de dates, de caractéristiques techniques de l’appareil photo utilisé, de géolocalisation, de droits d’auteur ou encore de programmes tiers utilisés pour modifier le fichier (Photoshop…).

Le nombre de données EXIF effectivement fournies, ainsi que leur disposition, varie considérablement d’un appareil photographique à l’autre, voire même, pour un appareil donné, selon le micrologiciel (« firmware ») utilisé.

Malheureusement, l’étude seule de ces métadonnées ne suffit pas à démontrer la présence d’une éventuelle supercherie. En effet, elles sont facilement modifiables et peuvent également être intégralement remplacées grâce à l’utilisation de logiciels spécialisés, tels qu’EXIFer, EXIFtool ou même un simple éditeur de texte en hexadécimal.

Une bonne approche cependant - et un travail préliminaire utile - consiste à comparer les données EXIF du document photographique étudié avec celles extraites d’une autre photographie prise avec le même appareil, si possible comportant le même firmware. Dans un grand nombre de cas, cette simple vérification permet de mettre en évidence l’utilisation d’un programme de retouche.

Sur un document qui n’est pas original, cela n’a aucune valeur intrinsèque, tant il existe diverses façons involontaires de modifier les métadonnées. Cependant, sur un document de première main et original (ou affirmé comme tel par le témoin), cela peut permettre l’invalidation de l’authenticité du document.

Autres métadonnées et marqueurs

Il existe beaucoup d’autres métadonnées associées aux photos/vidéos numériques (IPTC, XPM…), plus ou moins connues et faciles à extraire. Leur exploitation par un outil d’authentification spécialisé, comme IPACO, permet de vérifier si le document est ou non un original. S’il ne l’est pas, il appartient à l’analyste de déterminer s’il y a eu manipulation des données ou non. Pour des raisons évidentes, nous n’entrerons pas davantage ici dans les détails.

Paramètres de compression du fichier

La plupart des photographies numériques sont enregistrées dans le format JPEG, qui utilise des algorithmes de compression avec perte irréversible.

Concrètement, cela se traduit par une modification des tables de quantification lorsqu’il y a intervention d’un programme tiers et/ou une nouvelle sauvegarde du fichier. Cette modification peut être détectée grâce à l’utilisation de logiciels spécialisés, tels que JPEGSnoop, qui est capable d’extraire toutes les données propres à divers formats (outre le JPEG, il traite aussi les formats AVI, MOV pour les vidéos, et nombre de formats RAW : NEF, THM, DNG…) et de les comparer à une base de données interne comprenant la signature de compression de nombreux appareils photos et logiciels.

Dans la majorité des cas, l’application combinée de tout ou partie des techniques décrites ci-dessus sur des documents falsifiés permet de mettre à jour la supercherie.

Photo-interprétation de l’image

Une fois le fichier image chargé sur son ordinateur, l’analyste pourra le découvrir et se familiariser avec lui à l’aide d’un logiciel spécialisé en visualisation ou en traitement d’images. En mettant en évidence des détails de l’image, il pourra tenter de faire des rapprochements entre cette photo et des cas déjà rencontrés, de déceler d’éventuels indices et de dégager des pistes de réflexion pour aborder une analyse quantitative plus approfondie.

Les outils de manipulation d’image les plus utiles sont aussi les plus classiques : zoom, renforcement de contraste, filtres de netteté (passe-haut), détection de contours, séparation ou renforcement des couleurs primaires.

Les logiciels utilisables pour un tel travail sont multiples. La référence la plus connue est Photoshop, logiciel extrêmement riche en fonctionnalités interactives et principalement destiné aux photographes. Une première approche est également possible avec des outils de visualisation plus simples tels que le logiciel Irfanview.

La solution la mieux adaptée est celle d’un outil de PIAO, qui permet par définition de réaliser simultanément la photo-interprétation interactive (objet de ce paragraphe) et l’analyse quantitative (objet du paragraphe suivant), dans une démarche souple et efficace. C’est le cas du logiciel IPACO.

Illustration : la manipulation interactive de la photo de Chambley a essentiellement consisté à utiliser le zoom, en tirant profit de la haute résolution du document original (10 mégapixels).

À ce stade, on peut imaginer qu’il puisse s’agir d’un ballon d’enfant, ou à la rigueur d’un très gros oiseau.

Analyse quantitative de l’image

Mesures géométriques

Les mesures géométriques sur une photo numérique reposent sur la localisation de pixels dans l’image, qui permet de remonter à la position de points d’intérêt sur le support photosensible (matrice de photosites), et de là à la position angulaire des points correspondants dans la scène étudiée.

L’opération de base consiste donc à désigner un point sur l’écran à l’aide de la souris et à recueillir ses coordonnées (colonne et ligne). Cela peut être effectué sur l’image telle quelle, en pleine résolution (sa taille étant toujours supérieure à celle de l’écran, on aura recours aux ascenseurs de la fenêtre pour la parcourir entièrement), ou en utilisant un zoom, qui permet de réaliser un pointé avec plus de précision et, parfois, de localiser le point d’intérêt à mieux qu’un pixel près.

Les coordonnées d’un point A en pixels sont fournies sous la forme A {ia,ja}, avec :

ia  : numéro de colonne, de gauche à droite de l’écran, compris entre 0 et H-1

ja  : numéro de ligne, de haut en bas de l’écran, compris entre 0 et V-1

H  : nombre total de colonnes (donc de pixels à l’horizontale)

V  : nombre total de lignes (donc de pixels à la verticale)

Les coordonnées du centre P de la photo étant  P {(H-1)/2,(V-1)/2}, on en déduit les distances en pixels entre P et deux points A et B :

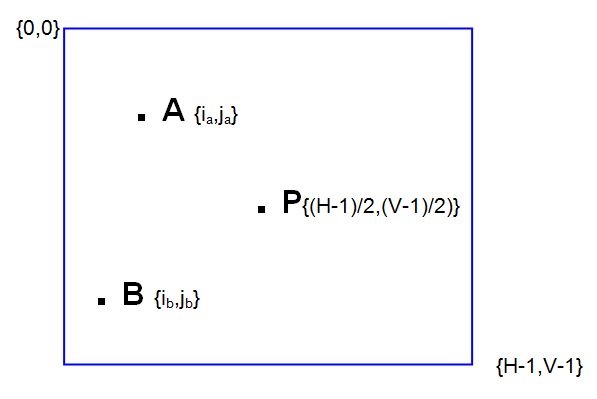
PA =  √ { [ia - (H -1)/2]2 + [ja - (V-1)/2]2 }

PB =  √ { [ib - (H -1)/2]2 + [jb - (V-1)/2]2 }

AB =  √ { (ia - ib)2 + (ja - jb)2 }

Ces distances en pixels peuvent alors être converties en distances réelles sur le support photosensible, par simple application d’une règle de 3, si l’on dispose des dimensions physiques réelles de ce support.

Les dimensions de la matrice photosensible peuvent être obtenues directement avec les caractéristiques techniques de l’appareil, ou déduites du coefficient de conversion de focale, si celui-ci est fourni, soit avec ces caractéristiques, soit avec les métadonnées EXIF associées à la photo (cela dépend des constructeurs).

Il faut garder à l’esprit que ce coefficient de conversion s’applique à la diagonale des rectangles (ou carrés) que constituent les capteurs. Généralement, il correspond au ratio de la diagonale du format argentique standard 24x36 mm – soit 43,3 mm – par la diagonale de la matrice de photosites de l’appareil numérique.

À partir des dimensions réelles sur le support photosensible et de la longueur focale, les différents calculs de dimensions angulaires, puis les éventuelles estimations de dimensions absolues peuvent être effectués (cf. plus haut).

En ce qui concerne les estimations de la distance séparant l’objet étudié de l’appareil de prise de vue, certaines approches (cf. plus haut) nécessitent des mesures radiométriques ou des estimations de netteté. On se reportera alors respectivement aux deux paragraphes suivants.

Illustration : les mesures de tailles angulaires intéressantes sur la photo de Chambley concernent la plus grande dimension apparente de l’objet non identifié (nous parlerons de sa « longueur ») et les montgolfières (nous nous intéresserons au diamètre horizontal de deux d’entre elles).

Le logiciel IPACO permet de calculer directement en quelques clics ces tailles angulaires, en exploitant automatiquement les données EXIF disponibles. Mais à des fins pédagogiques, nous décomposons ici les calculs pas à pas.

D’abord, nous relevons interactivement les coordonnées des 6 pixels désignés dans l’image ci-dessous (taille de l’image : 3872 colonnes, 2592 lignes) :

Extrémités de l’objet étudié :  A {550,371}     B {582,368}

Extrémités latérales du ballon 1 :  C {591,1753}       D {841,1753}

Extrémités latérales du ballon 2 :  E {1864,1288}     F {2689,1288}

Le calcul de la taille angulaire de l’objet non identifié est le suivant, en se référant aux formules indiquées précédemment (où P est le centre de la photo) :

PA = √ { (550 – 1935,5)2 + (371 – 1295,5)2 }   = 1666 pixels

PB = √ { (582 – 1935,5)2 + (368 – 1295,5)2 }   = 1641 pixels

AB = √ { (550 – 582)2 + (371 – 368)2 }            =    32 pixels

La longueur focale étant de 80 mm (métadonnée EXIF), et le coefficient de conversion de focale étant égal à 1,5 (donnée technique de l’appareil), on se ramène au cas d’un appareil 24x36 mm équipé d’une focale de longueur  f = 120 mm (autre métadonnée EXIF appelée « Longueur focale équivalente 35mm »).

Dans ce cadre (24x36 mm), la dimension effective d’un pixel est égale à :

36/3871 ≈ 24/2591 ≈ 0,00928 mm

d’où :

a = PA = 15,46 mm

b = PB = 15,23 mm

d = AB =   0,30 mm

Par application de la formule de Pythagore généralisée (cf. plus haut), on peut calculer la taille angulaire de l’objet non identifié :    

            objet = arccos [(2x1202+15,462+15,232–0,302) / 2√{(1202+15,462)(1202+15,232)}]

 objet = 0,14 °

De la même façon, on calcule la taille angulaire (diamètre horizontal) des deux ballons de référence :

 ballon1 = 1,10 °

 ballon2 = 3,65 °

Estimations de luminance

Les données directement mesurables qui quantifient la lumière reçue par un pixel donné de l’image numérique sont celles du niveau de gris (en noir et blanc) ou des niveaux respectifs dans les 3 couleurs primaires (rouge, vert, bleu). Ces valeurs traduisent la luminance apparente des points correspondants de la scène, mais avec certaines limitations (cf. plus haut).

On ne peut donc, dans ce domaine, que faire des estimations et des classements par valeurs croissantes ou décroissantes de luminance apparente. Cela peut néanmoins suffire pour réaliser une interpolation approximative et estimer une fourchette de distances possibles entre un objet et l’objectif.

On utilisera, pour ce type de mesure, un logiciel de visualisation ou de traitement d’image permettant de recueillir les niveaux associés à un pixel désigné sur l’écran à l’aide de la souris, ou la répartition des valeurs de ces niveaux sur une zone donnée de l’image, sélectionnée graphiquement sur l’écran, ou encore le tracé de l’évolution de ces niveaux le long d’un segment désigné (coupe radiométrique).

Voici des exemples illustrant ce type de mesures, à l’aide du logiciel IPACO :

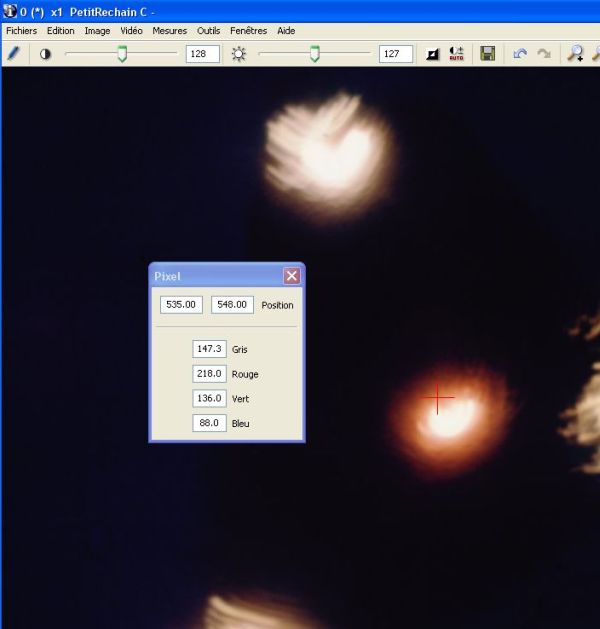
À la position du curseur (croix rouge) correspondent les coordonnées du pixel désigné, ainsi que ses niveaux RVB (rouge, vert, bleu) et gris (moyenne des 3).

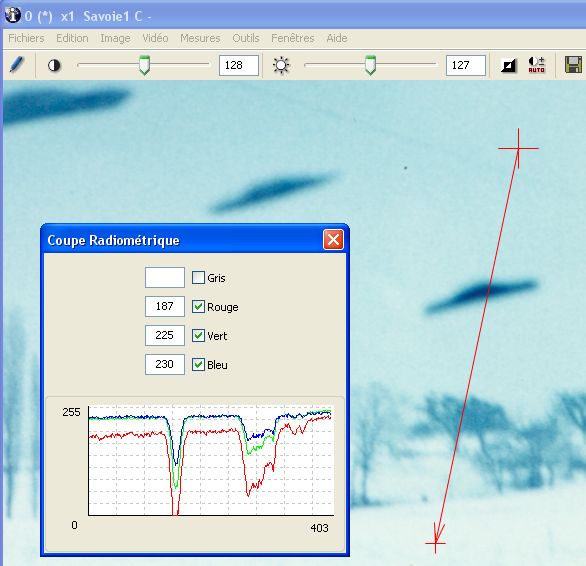
Au vecteur tracé à droite de l’image (flèche rouge) correspond la coupe radiométrique qui présente les niveaux (traduisant la luminance apparente), affichée dans la fenêtre.

Illustration : la photo de Chambley est prise à contre-jour et on peut considérer que les parties les plus sombres des objets de la scène sont soumises aux variations de luminance apparente essentiellement dues à la diffusion atmosphérique. On s’intéressera donc à la partie sombre de l’objet étudié, ainsi qu’aux parties sombres des nacelles des deux ballons de référence.

Dans une approche très empirique, on se contentera de relever les valeurs respectives des pixels les plus sombres dans chacune de ces trois zones, en utilisant à cette fin, sous IPACO, l’outil d’analyse de la radiométrie des pixels inclus dans une surface fermée (ici un cercle rouge).

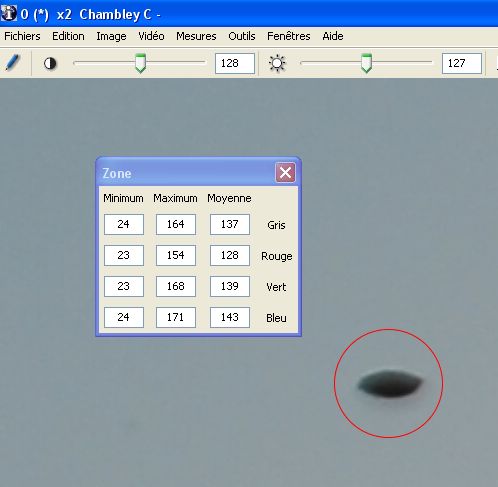
Niveau sombre objet = 24

On fera de même pour les nacelles des 2 ballons de référence.

Ballon 1 :

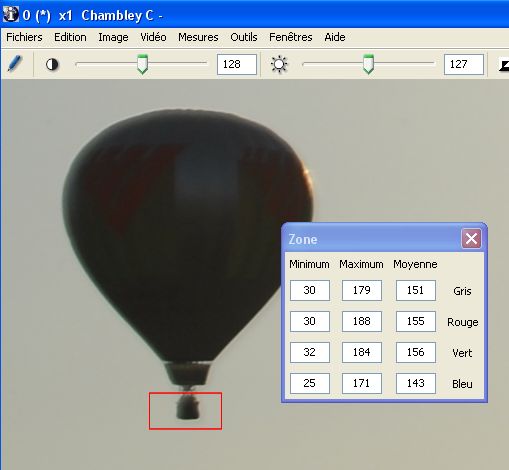
Ballon 2 :

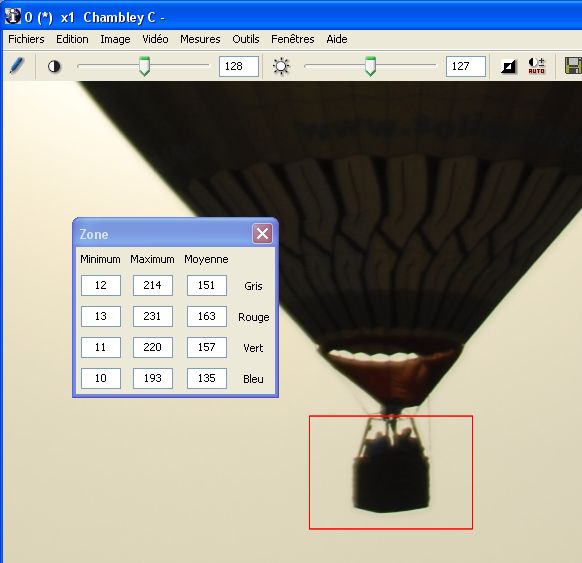
Niveau sombre ballon1 = 30           Niveau sombre ballon2 = 12

En faisant l’hypothèse – vraisemblable – que l’objet étudié et les deux nacelles de référence sont bien des corps sombres, on déduit que l’objet se trouvait à une distance de l’appareil photo comprise entre celle du ballon 1 et celle du ballon 2. Or ces distances peuvent être évaluées, si l’on suppose que ces deux ballons ont un diamètre standard Ф = 15 m, à l’aide de la formule déjà évoquée (cf. plus haut) :

Distance ballon1 = (Ф/2) / tan ( ballon1 / 2)    soit :  Distance ballon1 = 391 m

Distance ballon2 = (Ф/2) / tan ( ballon2 / 2)    soit :  Distance ballon2 = 118 m

En interpolant linéairement sur les niveaux des pixels les plus sombres (approche empirique), on obtient une estimation de la distance de l’objet non identifié :

Distance objet = 300 m

On en déduit une estimation de sa longueur réelle :

Longueur objet = 2 x 300 tan (0,14°/2)    soit :

Longueur objet = 0,73 m

Compte tenu des incertitudes et des approximations de calcul, on conclura avec prudence que la longueur de l’objet – s’il était réellement sombre – devait être comprise entre 50 cm et 1 m.

(S’il avait été - en réalité - plus clair, sa longueur n’aurait pu être qu’inférieure à cette évaluation).

Évaluation de la netteté (FTM)

L’évaluation de la netteté des contours d’un objet, en dehors du cas d’un flou de bougé (qui doit être analysé au cas par cas), peut être requise pour l’estimation de la distance de cet objet, dans le cadre de deux démarches distinctes.

D’une part, si l’objet se trouvait en dehors de la profondeur de champ, il apparaît forcément plus flou sur la photo que les objets situés à l’intérieur de cette profondeur. Cela est en particulier le cas pour de tout petits objets situés très près de l’appareil, surtout s’ils sont illuminés par un flash (voir de nombreux dossiers photographiques montrant des « orbes »).

D’autre part on constate parfois, à l’intérieur de la profondeur de champ, que la netteté apparente des contours d’un objet se détériore progressivement au fur et à mesure que cet objet s’éloigne, en raison de la diffusion atmosphérique : la couche d’atmosphère traversée est caractérisée par sa FTM (Fréquence de Transfert de Modulation), qui agit comme un filtre passe-bas dans le domaine des fréquences spatiales, ce phénomène étant plus ou moins mesurable en fonction des conditions météorologiques. La comparaison des contours de l’objet étudié avec ceux d’autres objets situés à des distances connues ou estimées de l’appareil permet alors de resserrer la plage des distances possibles.

Le seul moyen empirique simple d’estimer la netteté d’un contour est de visualiser une coupe radiométrique (de la même nature que la coupe densitométrique pratiquée en photographie argentique) perpendiculaire à ce contour. En effet, le spectre de fréquences spatiales est lié par transformation de Fourier, dans l’espace bidimensionnel de l’image, à la réponse impulsionnelle (image restituée d’une source de lumière ponctuelle), qui elle-même peut être approchée sous forme monodimensionnelle par la réponse, dans une direction donnée, à la fonction « marche d’escalier » que constitue la discontinuité du contour d’un objet.

En pratique, plus la courbe de transition des niveaux de gris, de part et d’autre d’un contour, s’étale sur une grande largeur en pixels (autrement dit : plus la pente de la transition est faible), plus l’image a été dégradée par la FTM de l’atmosphère, donc plus l’objet se trouvait éloigné (épaisseur atmosphérique plus importante), toutes choses étant égales par ailleurs.

Là encore, il n’est souvent possible d’envisager qu’une interpolation approximative entre les « réponses » des contours de plusieurs objets de la scène, permettant de les « classer » par ordre de distance croissante.

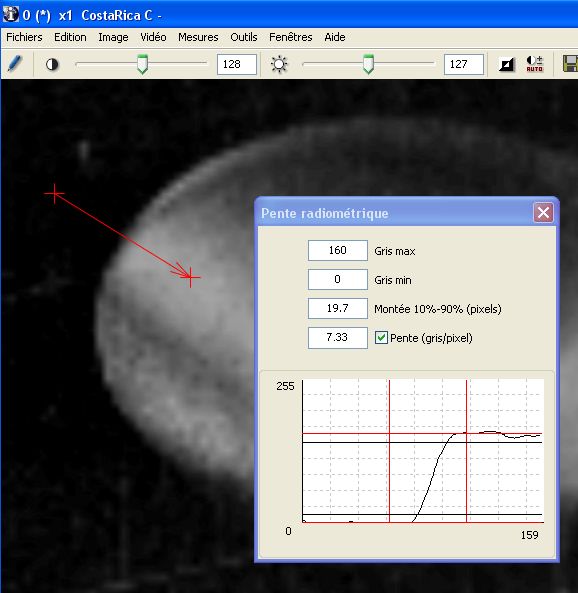
Estimation de la pente radiométrique le long d’un vecteur désigné, perpendiculaire au contour de l’objet analysé : la pente de la transition est ici évaluée à 7,33 niveaux/pixel (transition de 10% à 90% sur 19,7 pixels).

Illustration : les conditions météorologiques de la photo de Chambley, avec une excellente visibilité, ne permettent pas la mise en évidence d’une dégradation de la netteté des contours (FTM) par la diffusion atmosphérique (les pentes maximales de coupes radiométriques perpendiculaires aux contours respectifs de l’objet non identifié et des deux ballons de référence sont du même ordre de grandeur).

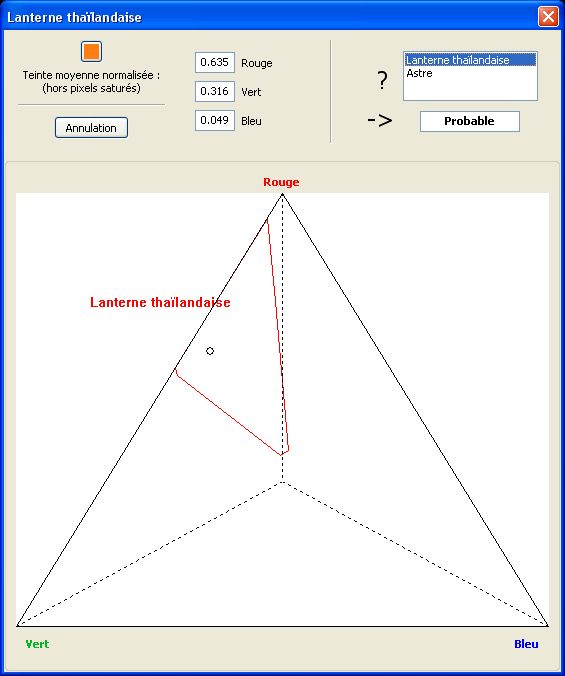
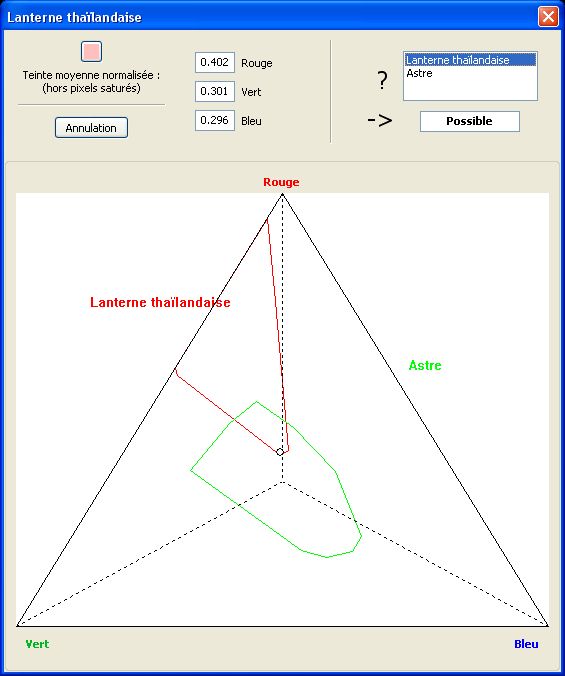
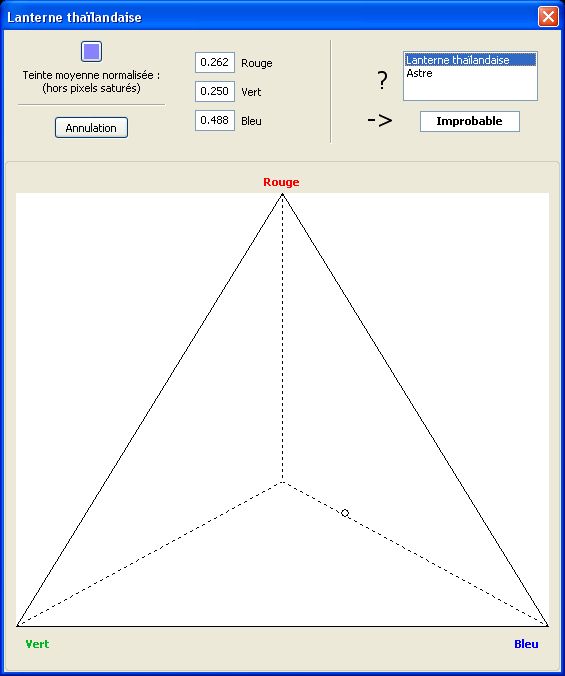
Comparaison des couleurs

L’analyse colorimétrique est un domaine particulièrement complexe dans lequel nous ne nous risquerons qu’à deux petits axes de réflexion particuliers.

D’une façon très macroscopique, il arrive parfois qu’une photo ait une nette dominante colorée (bleu, vert, magenta, etc.). Si un objet non identifié est présent sur la photo, mais avec une couleur dominante très différente de celle du reste de la scène, il y a de fortes présomptions pour que l’image résulte d’un trucage par incrustation. En effet, pour qu’un petit objet à forte dominante magenta puisse apparaître sur un fond de paysage à forte dominante verte, par exemple, il faudrait que l’énergie lumineuse émise par cet objet soit quasiment infinie (sans quoi sa propre couleur devrait apparaître grise ou blanche).

Dans un autre ordre d’idées, l’information de couleur concernant un objet non identifié peut être utile pour étayer ou réfuter l’hypothèse d’un type donné d’énergie émise (mode de propulsion par exemple), ou pour mettre en évidence un phénomène physique connexe, tel que l’ionisation de l’air ambiant.

Prise en compte éventuelle de la texture

Si l’objet analysé apparaît avec une taille angulaire suffisante, et s’il présente au moins une face d’aspect homogène, il se peut que celle-ci soit caractérisée par une texture particulière, qu’on pourrait mettre en évidence à l’aide d’un zoom et/ou d’un filtre passe-haut (renforçant les contrastes).

Cette texture devra dans ce cas être rapprochée de catalogues de textures, caractérisant différents types de matériaux.

Existence d’un stimulus externe

L’existence d’un stimulus extérieur à l’appareil de prise de vue sera établie par élimination des différentes causes internes possibles.

Les causes internes habituelles peuvent être énumérées, en partant de la liste déjà connue pour les photos argentiques, à l’exception des problèmes mécaniques ou chimiques affectant le film, qui n’ont pas leur équivalent en numérique :

• Exposition multiple (superposition de 2 ou plusieurs prises de vues) : ce problème, fortuit ou voulu, se présente parfois en photographie argentique, et peut d’ailleurs être mis en évidence par un examen approfondi (au microscope) de la disposition et de la taille des grains sur le film (leur taille croît en fonction du nombre d’expositions). Mais en dehors de certains appareils, qui offrent une possibilité d’exposition multiple voulue, ce type d’accident est exclu la plupart du temps, par construction, en photographie numérique.

• Réflexions optiques parasites : selon la configuration du bloc optique dans l’appareil et la présence ou non de traitement antireflet sur l’objectif, des réflexions parasites peuvent parfois survenir à côté de l’image d’une source lumineuse, laissant souvent apparaître un contour polygonal (diaphragme). Ils sont en général assez faciles à mettre en évidence.

Il existe aussi, en présence de sources lumineuses intenses (soleil, projecteur) des cas de réflexions multiples et complexes laissant apparaître des formes lumineuses parasites complexes très arrondies, rappelant parfois les courbes mathématiques appelées caustiques. Ces reflets (ou « flares ») sont reconnaissables au fait qu’ils apparaissent dans des positions symétriques des sources lumineuses, par rapport au centre optique de la photo.

À titre d’exemple, le cliché ci-dessous, pris de nuit dans une rue de Toulon, montre une accumulation inhabituelle d’effets d’optique.

• Fuites de lumière : lorsque l’obturateur présente un défaut de fermeture, il laisse parfois passer un peu de lumière, ce qui se traduit par des photos où apparaît une traînée de lumière de forme quelconque (reflétant le mouvement de l’opérateur juste après sa prise de vue) qui semble émaner d’une source lumineuse. Cette traînée apparaît même en pointillés lorsque la source est une ampoule électrique alimentée en courant alternatif (50 Hz) et que le mouvement de l’opérateur a été suffisamment rapide.

• Défaut de propreté de l’objectif : pour mémoire, si l’objectif est très sale ou rayé, les photos peuvent être dégradées, notamment en netteté (FTM). L’état de l’objectif peut être vérifié a posteriori.

• Pixel(s) défectueux : dans un appareil numérique, il arrive qu’un pixel soit endommagé, produisant alors systématiquement un point noir à son emplacement dans les photos. Ce type d’incident est facile à mettre en évidence par rapprochement entre plusieurs photos issues du même appareil.

• Les défauts spécifiquement générés par l’algorithme de compression des images numériques (format JPEG) affectent essentiellement la couleur et consistent généralement en moirés apparaissant sur des surfaces relativement unies.

• Les montages photographiques par incrustation dans l’image d’un ou plusieurs éléments étrangers à la scène font évidemment partie des cas où il n’y avait aucun stimulus réel dans la scène.

La mise en évidence de ce type de supercherie doit s’appuyer sur des critères de cohérence : luminance, couleur, albédo, netteté (FTM), ombres, éventuel flou de bougé de l’opérateur.

Illustration : en ce qui concerne la photo de Chambley, on peut aisément exclure toutes les causes classiques de fausse manœuvre, ainsi que l’hypothèse d’un trucage, compte tenu de la technologie de l’appareil utilisé, de la démarche coopérative de son auteur et – principalement – de l’existence d’au moins un autre cliché pris indépendamment, et dont l’étude (non reproduite ici) montre une bonne cohérence avec les évaluations quantitatives présentées précédemment.

Présence d’un objet matériel dans le champ

La présence effective ou non d’un objet matériel dans la scène sera établie grâce à d’éventuels indices prouvant la réalité concrète de cet objet (couleur sombre, ombre portée, éclairage cohérent avec la scène par le soleil, la lune ou toute source lumineuse artificielle).

Si un objet se trouvait effectivement dans le champ de prise de vue, c’est-à-dire à l’intérieur de l’angle solide d’observation dont le sommet était le centre de l’objectif, il pouvait être ou ne pas être dans la profondeur de champ, qui définit la fourchette de distances à l’intérieur de laquelle les éléments de la scène apparaissent nets.

On procédera donc en premier lieu à un examen de la netteté des contours (FTM).

Illustration : la photo de Chambley montre un objet sombre, ce qui exclut d’emblée l’hypothèse d’un phénomène purement lumineux.

Tous les objets visibles dans la scène photographiée sont suffisamment éloignés de l’appareil de prise de vue, qui était focalisé à l’infini, pour que l’on soit certain qu’ils étaient tous à l’intérieur de la profondeur de champ.

Objet en dehors de la profondeur de champ

Si l’appareil de prise de vue était focalisé sur une courte distance, la profondeur de champ est située entre deux limites finies que l’on sait évaluer à partir des caractéristiques et des réglages. Un objet lointain peut, dans ce cas, apparaître flou, ce qui permet de déduire que sa distance était supérieure au maximum de la profondeur de champ, surtout si d’autres objets visibles permettent une comparaison.

La plupart du temps, les réglages sont faits (de façon fixe ou par l’opérateur) sur l’infini. Seuls des objets plus proches de l’objectif que le minimum de la profondeur de champ peuvent apparaître flous (en dehors d’un flou de bougé, qui affecte toute la scène). C’est notamment le cas pour les « orbes » : ces taches blanches circulaires correspondent le plus souvent à des poussières en suspension, des gouttelettes ou des insectes devant l’objectif, sous l’éclair du flash (Voir illustration suivante).

Ce type de tache floue circulaire apparaît plus fréquemment avec les appareils numériques, dont la profondeur de champ est plus importante qu’en argentique, et particulièrement avec les modèles compacts, dans lesquels le flash est géométriquement plus proche de l’objectif, éclairant ainsi les poussières ou autres petits insectes qui l’entourent.

Objet à l’intérieur de la profondeur de champ

Si l’objet étudié apparaît net, c’est qu’il se trouve à l’intérieur de la profondeur de champ. Cela permet d’évaluer, à partir de sa taille angulaire, une fourchette de tailles possibles (si la profondeur de champ a une limite supérieure) ou une taille minimum (si la profondeur de champ va jusqu’à l’infini).

Nature d’un phénomène identifié

Si l’objet ou le phénomène semble identifié, on recherchera à effectuer des mesures objectives et des rapprochements permettant d’en établir la démonstration formelle.

La qualité irréprochable de cette démonstration est d’une grande importance, car un classement en « phénomène identifié » revêt un caractère définitif, contrairement à un classement en « non identifié », toujours susceptible – par définition – d’être révisé.

Illustration : l’objet photographié à Chambley n’a pas été formellement identifié [ceci a été écrit en 2008], mais il pourrait éventuellement s’agir d’un ballon d’enfant légèrement dégonflé ou peut-être d’un gros oiseau. Seule une enquête approfondie sur place permettrait de déterminer le caractère plausible ou non de ces deux hypothèses.

Caractéristiques d’un phénomène non identifié

S’il n’est pas possible de déterminer la nature de l’objet étudié, la photo peut fournir des éléments de caractérisation : géométrie (taille, forme), photométrie (lumière émise, transmise ou réfléchie), couleur, texture, vitesse, accélération.

Rappelons à nouveau le grand intérêt scientifique qu’il y aurait à pouvoir disposer d’information spectrale plus riche qu’une simple photo en couleur sur la lumière issue des PAN, notamment lorsqu’ils semblent émettre leur propre énergie (cf. Remarque).

Cas d’un document vidéo numérique

L’analyse d’un document vidéo nécessite un outil logiciel permettant non seulement la visualisation de ce document, mais aussi l’accès à un certain nombre de fonctionnalités de base :

• Projection au ralenti et au pas à pas, arrêt sur image

• Extraction d’une image ou séquence d’images, sélectionnée pour analyse statique

• Désentrelacement d’une image.

Le fichier d’origine sera chargé sur ordinateur, visualisé très attentivement, en vue d’une première étape consistant à sélectionner la ou les images instantanées les plus riches en informations, ce qui permettra de commencer au mieux l’analyse comme celle d’une photo issue d’un appareil photo numérique.

Si la rapidité des mouvements l’exige, on procédera au désentrelacement de certaines images, permettant une analyse temporelle plus fine.

Si les mouvements de l’objet sont significatifs, on pourra procéder au coup par coup à des évaluations de vitesse et d’accélération angulaires transversales.  

Si par ailleurs on se trouve dans les conditions - déjà évoquées - où il est possible d’estimer la distance entre l’objet non identifié et l’objectif (ou une fourchette de distances), on en déduira pour cet objet des estimations de taille réelle, de vitesse et d’accélération transversales.

Au cours de l’analyse dynamique de la vidéo, on évaluera également, s’il y a lieu, d’éventuels changements de taille, de forme ou de couleur.

ÉPILOGUE Illustration  

Quelques mois après la remise officielle au CNES/GEIPAN de la version initiale du rapport Chambley, l’enquête menée sur le terrain par M. Comtesse aboutissait : l’objet photographié était bien un gros ballon d’enfant, parfaitement identifié, dont la taille et la distance étaient conformes, à quelques pour cent près, aux conclusions de l’analyse de la photo.

Rapport final de M. Comtesse

OUTILS SPÉCIFIQUES POUR L’ÉTUDE DES OVNIS

Reflets optiques

Sur une photo (notamment nocturne), il arrive qu’apparaissent des formes lumineuses étranges qui résultent de réflexions parasites dans l’optique de l’appareil. Chacun de ces reflets provient d’une source lumineuse, qui se trouve presque toujours dans le champ de la prise de vue, et qui est donc visible sur la photo (dans certains cas rares, cependant, la source lumineuse peut se situer juste en dehors du champ). La caractéristique d’un reflet optique est qu’il se situe, dans le plan de la photo, sur la droite qui relie le centre optique de cette photo à la source lumineuse.

La plupart du temps, le centre optique d’une photo coïncide avec son centre géométrique. Il est alors aisé, pour vérifier si une tache lumineuse est un reflet optique, de tracer la droite reliant cette tache au centre de la photo, et de voir si cette droite traverse une source lumineuse. Si plusieurs reflets optiques sont visibles sur la même photo, le faisceau des droites qui les relient respectivement au centre traverse l’ensemble des sources lumineuses dont ils sont issus.

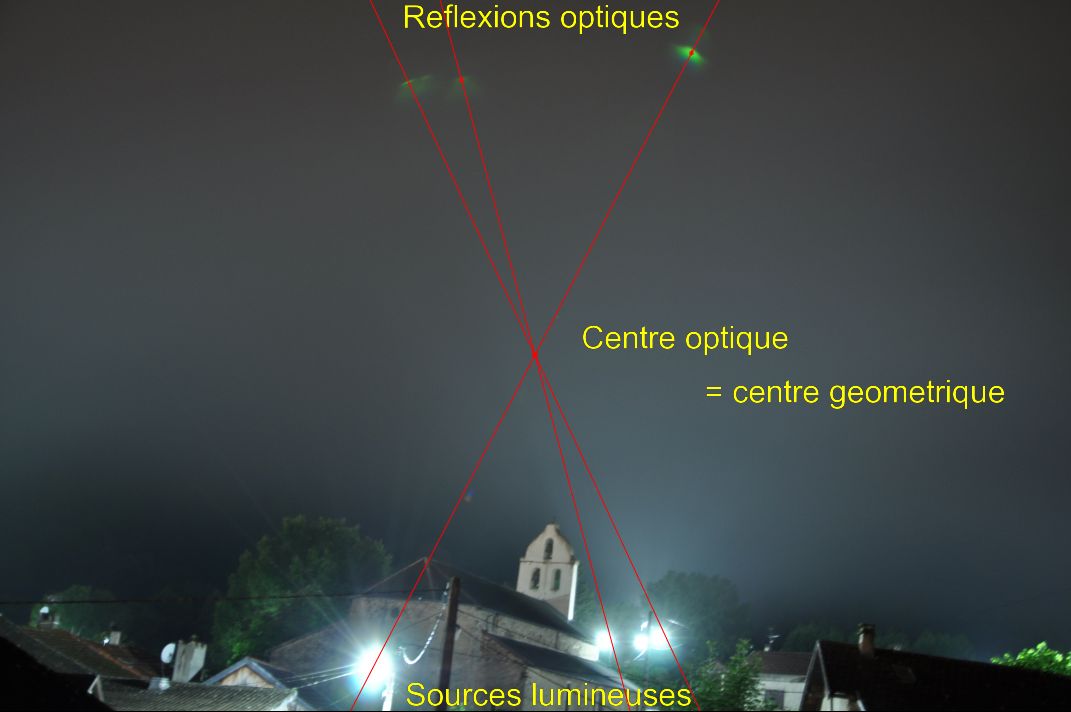
Si la droite qui relie une tache lumineuse au centre géométrique de la photo ne passe pas exactement par une source lumineuse, et s’il existe d’autres taches susceptibles d’être des reflets optiques, il est possible à la fois de le vérifier et de localiser le centre optique (qui, dans ce cas, est décalé par rapport au centre géométrique), en déplaçant interactivement la position du « centre » et en observant les mouvements qui en résultent pour le faisceau des droites qui le relient aux différentes taches : si une position est trouvée (empiriquement) pour le centre optique, telle que chaque droite du faisceau relie une tache à une source lumineuse, la démonstration est faite qu’il s’agit bien de reflets optiques.

Fil de suspension

La mise en évidence d’un type classique de supercherie, par photographie d’une maquette suspendue à un fil, est parfois délicate, voire impossible, selon la finesse du fil employé et son éloignement. Dans certains cas, des outils classiques de traitement d’image permettent de visualiser le fil (renforcement de contraste, filtrage passe-haut), mais cette approche se révèle souvent insuffisante.

Une méthode originale et plus puissante peut être utilisée, notamment si, dans la zone de présence supposée du fil, le fond du ciel est relativement uniforme et peut être assimilé à un « bruit » (bruit lié à la diffusion atmosphérique et/ou bruit de numérisation). Cette méthode consiste à augmenter le rapport signal sur bruit en additionnant les pixels de colonnes parallèles au fil, dans une zone choisie située au-dessus de l’ovni présumé.

Les étapes suivies par l’outil Fil vertical implanté dans le logiciel IPACO sont les suivantes, appliquées à l’une des célèbres photos de McMinnville :

1. Désigner un rectangle vertical au-dessus de l’ovni, couvrant la zone de présence supposée d’un fil. Une courbe s’affiche dans une fenêtre, représentant le niveau moyen des pixels de chaque colonne du rectangle.

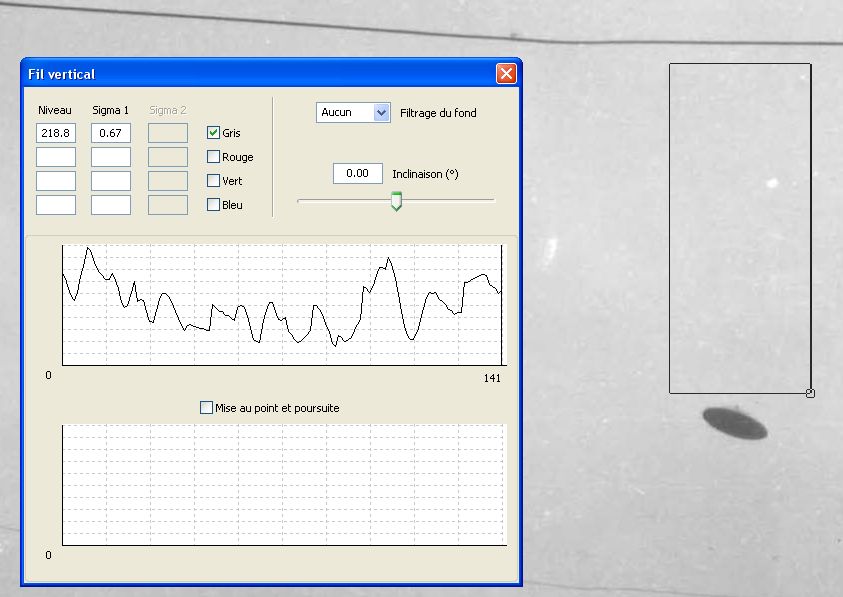
2. Déplacer simultanément une poignée le long du côté inférieur du rectangle, sur l’image, et une barre verticale à la position correspondante de la courbe. Positionner la poignée à l’emplacement du point d’accrochage présumé du fil. S’il existe un fil parfaitement vertical par rapport à la photo, et si l’augmentation du rapport signal sur bruit obtenue le permet, la courbe présente un pic à l’emplacement de la barre, positif ou négatif en fonction des couleurs comparées du fil et du fond de ciel. La valeur moyenne des pixels de la colonne correspondant à la position de la barre est constamment affichée, ainsi que l’écart entre cette valeur et la moyenne de la courbe, normalisé par l’écart-type (nombre de sigma).

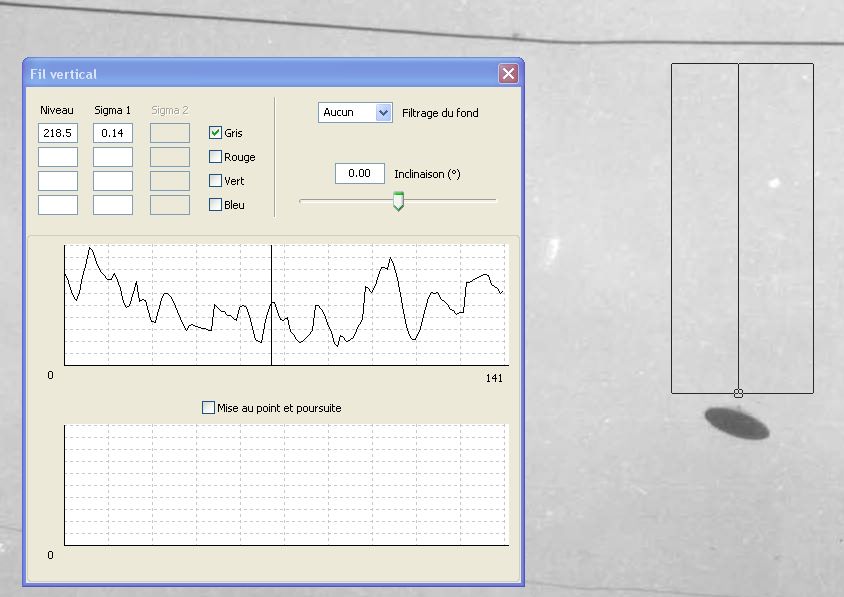
3. En général, cependant, le fil n’est pas strictement parallèle à l’axe vertical de la photo et rien de significatif n’apparaît à ce stade. L’outil permet alors de faire pivoter le rectangle de référence, d’un angle compris entre -30° et +30° par rapport à la verticale. Plus précisément, le rectangle se transforme en un parallélogramme, dont le côté inférieur reste fixe et la hauteur constante. Les colonnes de sommation des pixels sont inclinées du même angle, et la courbe se transforme au fur et à mesure des variations de l’angle.

4. Il est alors possible de vérifier visuellement s’il existe une valeur d’angle pour laquelle apparaît un pic significatif en face de la position supposée du point d’accrochage. Un tel pic indique une probabilité d’existence d’un fil, d’autant plus forte que l’écart entre ce pic et la moyenne est important.

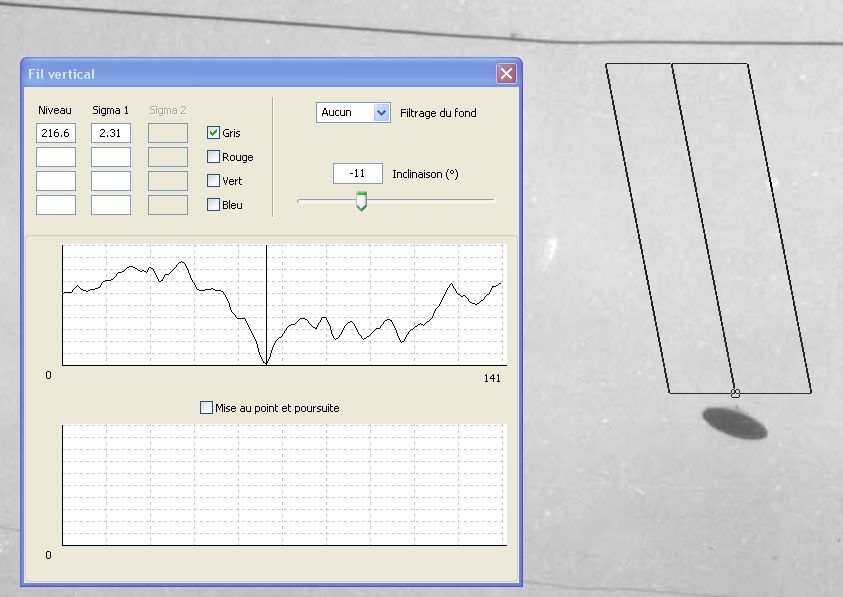
5. Si la courbe présente des variations lentes, par exemple dues au vignettage, il est possible de s’en affranchir par un filtrage spatial passe-haut, réalisé en lui soustrayant une copie d’elle-même préalablement lissée par filtre spatial passe-bas (convolution par une fenêtre rectangulaire). On obtient ainsi une valeur d’écart-type plus significative.

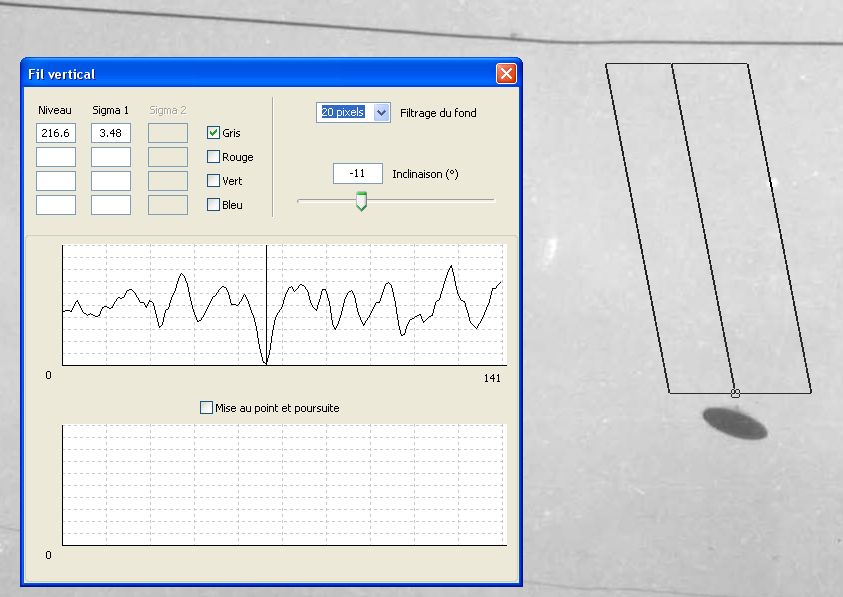
6. Si un tel pic est présent, l’outil peut lancer une optimisation automatique qui réglera finement l’angle d’inclinaison et la position de la barre, pour obtenir un écart maximum entre le pic et la moyenne.

7. Si les résultats vont dans le sens d’une confirmation de l’existence d’un fil, l’outil permet également une vérification supplémentaire. A partir de la droite calculée comme la plus probable pour l’emplacement du fil, et de la position présumée du point d’accrochage sur cette droite, un balayage circulaire est opéré autour de ce point, et les pixels des colonnes prises en compte pour la sommation sont ceux compris à l’intérieur du parallélogramme. Une seconde courbe s’affiche dans la fenêtre, représentant la variation du niveau moyen des pixels de chaque colonne au cours du balayage. Si un autre pic apparaît, correspondant à l’angle trouvé précédemment, la probabilité d’existence d’un fil est doublement établie, et ceci d’autant plus que le nouvel écart calculé entre le pic et la moyenne sur la seconde courbe est important.

Lanternes thaïlandaises

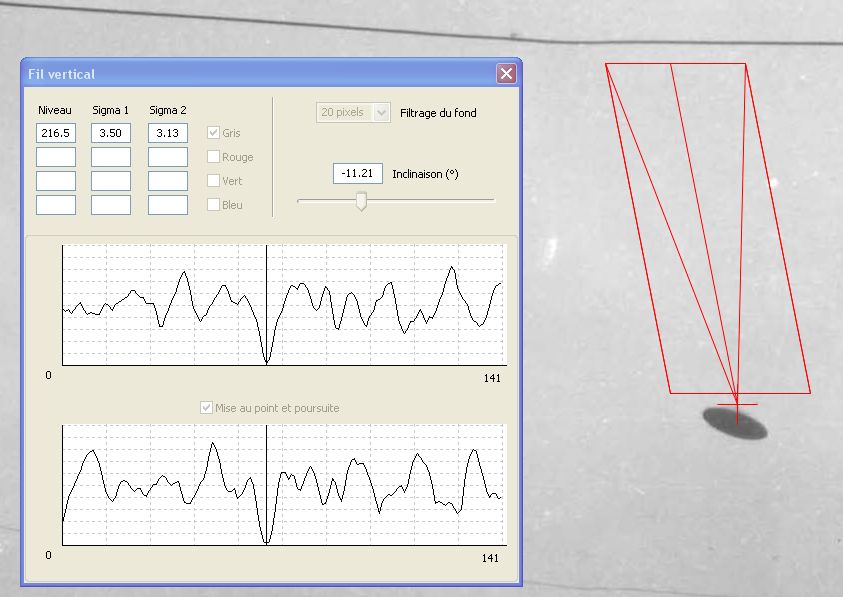
Les lanternes thaïlandaises sont une des causes de confusion les plus répandues à l’heure actuelle. Afin d’aider l’analyste à reconnaître ce type de source lumineuse dans une photo/vidéo nocturne, un outil spécifique a été mis en place dans IPACO. Celui-ci ne fournit pas de preuve formelle, mais donne une indication précieuse de probabilité d’explication par une lanterne thaïlandaise.

Le principe consiste à désigner la source lumineuse, calculer les niveaux moyens RVB des pixels non saturés de cette source, corrigés des valeurs du fond de ciel tout autour, et en déduire la chromaticité moyenne ce des pixels. Cette chromaticité est alors représentée dans le « triangle de Maxwell » et comparée à des zones caractéristiques de certains types de sources lumineuses (lanternes, étoiles/planètes, avions…). Ces zones ont été constituées à l’aide d’un très grand nombre de photos nocturnes du ciel montrant des sources lumineuses dont on connaît la nature, prises par une grande diversité d’appareils photos ou smartphones avec des réglages différents. Elles pourront être affinées au fil de l’exploitation.

Si la chromaticité moyenne de la source étudiée n’appartient qu’à la « zone lanternes », on considère l’explication par une lanterne comme probable. Si elle appartient à la « zone lanternes » et également à l’une des autres zones, l’explication par une lanterne est réputée possible. Si enfin elle n’appartient pas du tout à la « zone lanternes », l’explication par une lanterne est présentée comme improbable.

Retour<<

Le dossier présenté ici résulte de la mise à jour d’un rapport fourni contractuellement au CNES GEIPAN en 2008 :

APN & PAN - Méthodologie d’analyse des photos numériques de PAN

Si vous utilisez Internet Explorer (version 8 ou antérieure), cliquez sur le Bouton Compatibilité (Haut de l’écran) pour pouvoir lire les caractères spéciaux des formules.

SOMMAIRE

QUESTIONS SOULEVÉES PAR UNE PHOTO

Authenticité du document analysé

Réalité d’un stimulus extérieur à l’appareil de prise de vue

Présence effective d’un objet matériel dans la scène

Identification d’un phénomène

Caractérisation d’un phénomène non identifié

DEUX APPROCHES TECHNIQUES COMPLÉMENTAIRES

Analyse qualitative (Photo-interprétation)

Analyse quantitative (Mesures et estimations)

DONNÉES EXPLOITABLES

Environnement général de la prise de vue

Scène photographiée

Instrument et paramètres de prise de vue

Image numérique

PARAMÈTRES MESURABLES SUR UNE PHOTO

Paramètres géométriques

Paramètres radiométriques

ANALYSE D’UNE SÉQUENCE VIDÉO

Analyse image par image

Désentrelacement

Accumulation d’images

Analyse du mouvement

MÉTHODOLOGIE PRATIQUE D’ANALYSE

Recueil des données externes

Recueil des données techniques

Authentification du document

Photo-interprétation de l’image

Analyse quantitative de l’image

Existence d’un stimulus externe

Présence d’un objet matériel dans le champ

Nature d’un phénomène identifié

Caractéristiques d’un phénomène non identifié

Cas d’un document vidéo numérique

ÉPILOGUE Illustration

OUTILS SPÉCIFIQUES POUR L’ÉTUDE DES OVNIS

Reflets optiques

Fil de suspension

Lanternes thaïlandaises